J. Michael Fried - Mathematik für Ingenieure II für Dummies
Здесь есть возможность читать онлайн «J. Michael Fried - Mathematik für Ingenieure II für Dummies» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на немецком языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Mathematik für Ingenieure II für Dummies
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:5 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Mathematik für Ingenieure II für Dummies: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Mathematik für Ingenieure II für Dummies»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.

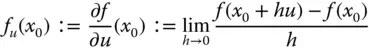
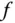 in Richtung
in Richtung 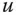 an der Stelle
an der Stelle 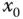 des Definitionsbereichs von
des Definitionsbereichs von 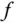 .
. in jede beliebige Richtung
in jede beliebige Richtung 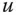 mit Hilfe der durch den Gradienten gegebenen totalen Ableitung direkt aus den Steigungen in Richtung der Koordinatenachsen, den partiellen Ableitungen, berechnen. Es ist
mit Hilfe der durch den Gradienten gegebenen totalen Ableitung direkt aus den Steigungen in Richtung der Koordinatenachsen, den partiellen Ableitungen, berechnen. Es ist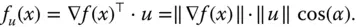
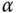 der Winkel zwischen dem Gradientenvektor
der Winkel zwischen dem Gradientenvektor 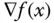 und dem Richtungsvektor
und dem Richtungsvektor 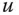 . Aus dieser einfachen Beziehung erhalten Sie eine interessante Schlussfolgerung:
. Aus dieser einfachen Beziehung erhalten Sie eine interessante Schlussfolgerung: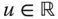 mit Betrag
mit Betrag 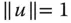 , dann ist die Steigung in Richtung des Gradienten maximal und senkrecht zur Gradientenrichtung minimal, da in diesen Fällen der Winkel
, dann ist die Steigung in Richtung des Gradienten maximal und senkrecht zur Gradientenrichtung minimal, da in diesen Fällen der Winkel 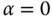 beziehungsweise
beziehungsweise 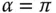 ist. Die Steigung verschwindet auf jeden Fall dann, wenn der Richtungsvektor
ist. Die Steigung verschwindet auf jeden Fall dann, wenn der Richtungsvektor 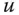 senkrecht auf dem Gradienten steht. In diesem Fall ist der Winkel
senkrecht auf dem Gradienten steht. In diesem Fall ist der Winkel 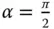 und daher
und daher 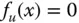 . In diese Richtung ist die Funktion
. In diese Richtung ist die Funktion 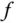 also konstant. Sie erhalten damit eine nützliche und anschauliche Beziehung zwischen dem Gradienten einer Funktion und ihren Höhenlinien.
also konstant. Sie erhalten damit eine nützliche und anschauliche Beziehung zwischen dem Gradienten einer Funktion und ihren Höhenlinien. Der Gradient
Der Gradient  einer differenzierbaren Funktion
einer differenzierbaren Funktion 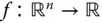 steht senkrecht auf den Höhenlinien von
steht senkrecht auf den Höhenlinien von 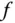 .
.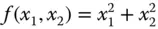
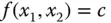 konzentrische Kreise mit Radius
konzentrische Kreise mit Radius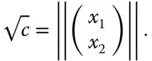
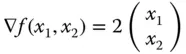
 steht der Vektor
steht der Vektor 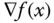 senkrecht auf dem Kreis mit Radius
senkrecht auf dem Kreis mit Radius 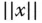 .
. einer einzigen Variablen kennen Sie wahrscheinlich nicht nur einfache, sondern auch mehrfache Ableitungen: Die Ableitung einer solchen Funktion
einer einzigen Variablen kennen Sie wahrscheinlich nicht nur einfache, sondern auch mehrfache Ableitungen: Die Ableitung einer solchen Funktion 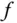 ist ihrerseits wieder eine reellwertige Funktion
ist ihrerseits wieder eine reellwertige Funktion 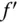 von einer Variablen, die Sie selbstverständlich auch auf Differenzierbarkeit untersuchen können. Falls die Ableitung
von einer Variablen, die Sie selbstverständlich auch auf Differenzierbarkeit untersuchen können. Falls die Ableitung 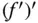 der Ableitungsfunktion existiert, erhalten Sie damit die zweite Ableitung
der Ableitungsfunktion existiert, erhalten Sie damit die zweite Ableitung 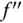 von
von 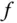 .
.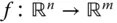 über die Ableitungen ihrer Ableitungen definieren.
über die Ableitungen ihrer Ableitungen definieren.










