 Eine Abbildung
Eine Abbildung 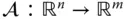 heißt affin lineare Abbildung , wenn sie als Summe einer gewöhnlichen linearen Abbildung
heißt affin lineare Abbildung , wenn sie als Summe einer gewöhnlichen linearen Abbildung 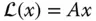 mit Matrix
mit Matrix 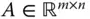 und eines konstanten Vektors
und eines konstanten Vektors 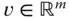 geschrieben werden kann.
geschrieben werden kann.
Mit dieser Definition bedeutet die Aussage
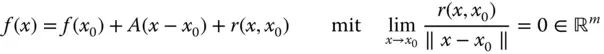
nichts anderes, als dass Sie 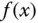 durch die affin lineare Abbildung
durch die affin lineare Abbildung
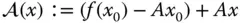
annähern können. Sie machen dabei einen Fehler 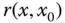 , der für
, der für  gegen null geht.
gegen null geht.
 Kurz gesagt: Nah der Stelle
Kurz gesagt: Nah der Stelle 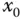 sieht eine (total) differenzierbare Funktion wie eine affin lineare Abbildung aus.
sieht eine (total) differenzierbare Funktion wie eine affin lineare Abbildung aus.
Je nach den Dimensionen der beteiligten Räume 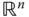 und
und 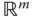 sehen die Jacobi-Matrizen unterschiedlich aus und entarten in zwei Spezialfällen sogar zu Vektoren:
sehen die Jacobi-Matrizen unterschiedlich aus und entarten in zwei Spezialfällen sogar zu Vektoren:
Der Fall : Die Abbildung beschreibt eine Kurve im -dimensionalen Raum. Die Ableitung entspricht einer sich im Kurvenpunkt an die durch beschriebene Kurve annähernden Geraden. Die Jacobi-Matrix ist in diesem Fall eine einspaltige Matrix: ein Spaltenvektor.
Der Fall : Es handelt sich hier um eine reellwertige Funktion von Veränderlichen. Stellen Sie sich dabei zum Beispiel eine Funktion vor, die die Temperatur (eine Zahl) an jedem Punkt im Raum beschreibt. Die Matrix entspricht in so einem Fall einem Zeilenvektor des , dem transponierten Gradienten :Mehr zum Gradienten einer reellwertigen Funktion finden Sie im Abschnitt »Praktische Berechnung der totalen Ableitung« weiter unten in diesem Kapitel.
Und geometrisch ist das auch!
Im Abschnitt »Differenzierbarkeit und Kurvendiskussion« in Kapitel 1wird die geometrische Bedeutung der Ableitung einer reellwertigen Funktion von einer reellen Variablen als Steigung der Tangente beschrieben. Genau wie im allgemeinen Fall im letzten Abschnitt können Sie im eindimensionalen Fall eine differenzierbare Funktion 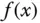 in der Nähe der Stelle
in der Nähe der Stelle 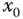 durch die affin lineare Funktion
durch die affin lineare Funktion
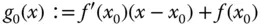
annähern: Diese affine Funktion ist die Tangente an den Graphen von 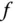 an der Stelle
an der Stelle 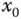 , die in Abbildung 2.4dargestellt ist.
, die in Abbildung 2.4dargestellt ist.
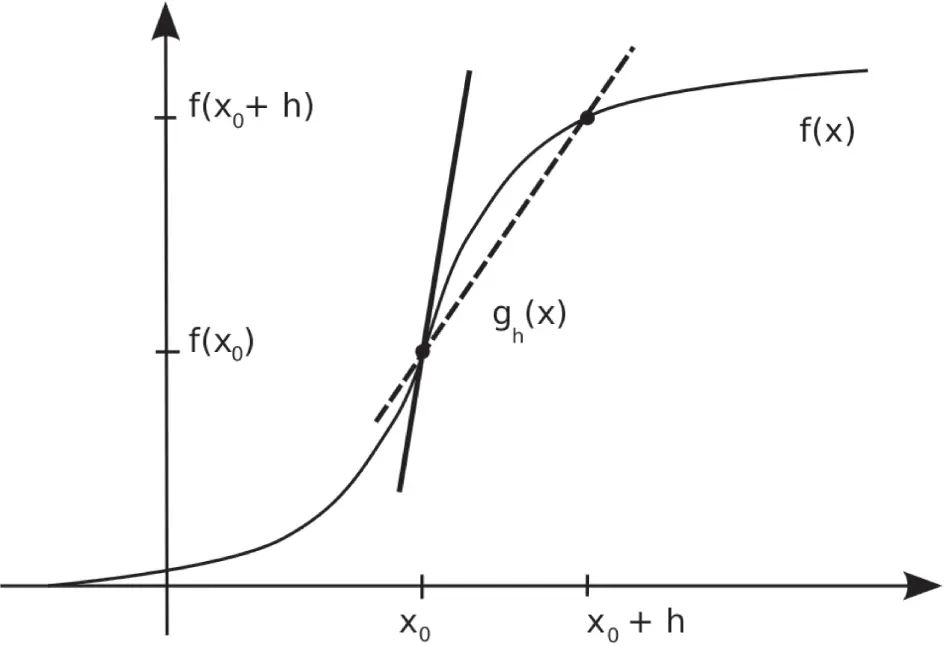
Abbildung 2.4: Die Tangente 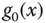 zum Graphen von
zum Graphen von 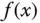 an der Stelle
an der Stelle 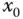
Die Jacobi-Matrix entspricht in diesem Spezialfall einer  -Matrix, also einer Zahl, nämlich der Ableitung
-Matrix, also einer Zahl, nämlich der Ableitung 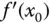 . Das ist nichts anderes als die Steigung der Tangente an den Graphen der Funktion
. Das ist nichts anderes als die Steigung der Tangente an den Graphen der Funktion 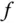 im Punkt
im Punkt 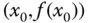 .
.
Wenn die Tangente in einer Umgebung von 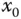 eine gute Approximation an die Funktion
eine gute Approximation an die Funktion 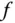 sein soll, muss
sein soll, muss
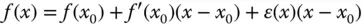
mit 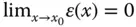 gelten, der Fehler
gelten, der Fehler  muss gegen null gehen, wenn Sie mit
muss gegen null gehen, wenn Sie mit 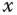 gegen den Punkt
gegen den Punkt 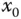 wandern.
wandern.
Читать дальше

 Eine Abbildung
Eine Abbildung 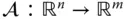 heißt affin lineare Abbildung , wenn sie als Summe einer gewöhnlichen linearen Abbildung
heißt affin lineare Abbildung , wenn sie als Summe einer gewöhnlichen linearen Abbildung 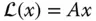 mit Matrix
mit Matrix 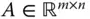 und eines konstanten Vektors
und eines konstanten Vektors 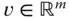 geschrieben werden kann.
geschrieben werden kann.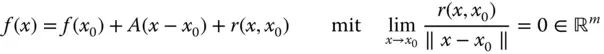
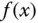 durch die affin lineare Abbildung
durch die affin lineare Abbildung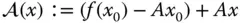
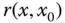 , der für
, der für  gegen null geht.
gegen null geht. Kurz gesagt: Nah der Stelle
Kurz gesagt: Nah der Stelle 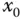 sieht eine (total) differenzierbare Funktion wie eine affin lineare Abbildung aus.
sieht eine (total) differenzierbare Funktion wie eine affin lineare Abbildung aus.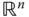 und
und 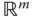 sehen die Jacobi-Matrizen unterschiedlich aus und entarten in zwei Spezialfällen sogar zu Vektoren:
sehen die Jacobi-Matrizen unterschiedlich aus und entarten in zwei Spezialfällen sogar zu Vektoren: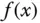 in der Nähe der Stelle
in der Nähe der Stelle 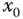 durch die affin lineare Funktion
durch die affin lineare Funktion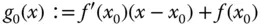
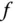 an der Stelle
an der Stelle 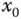 , die in Abbildung 2.4dargestellt ist.
, die in Abbildung 2.4dargestellt ist.
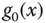 zum Graphen von
zum Graphen von 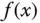 an der Stelle
an der Stelle 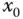
 -Matrix, also einer Zahl, nämlich der Ableitung
-Matrix, also einer Zahl, nämlich der Ableitung 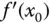 . Das ist nichts anderes als die Steigung der Tangente an den Graphen der Funktion
. Das ist nichts anderes als die Steigung der Tangente an den Graphen der Funktion 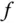 im Punkt
im Punkt 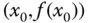 .
.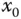 eine gute Approximation an die Funktion
eine gute Approximation an die Funktion 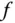 sein soll, muss
sein soll, muss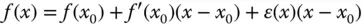
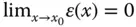 gelten, der Fehler
gelten, der Fehler  muss gegen null gehen, wenn Sie mit
muss gegen null gehen, wenn Sie mit 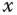 gegen den Punkt
gegen den Punkt 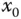 wandern.
wandern.










