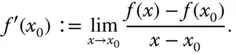
Anschaulich betrachtet man dabei das Grenzverhältnis in der Änderung des Funktionswerts 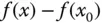 im Vergleich zur Änderung des Arguments
im Vergleich zur Änderung des Arguments 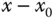 .
.
Prinzipiell wird die (totale) Ableitung auch für Abbildungen 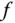 zwischen mehrdimensionalen Räumen so definiert, allerdings müssen Sie dabei beachten, dass die Änderung
zwischen mehrdimensionalen Räumen so definiert, allerdings müssen Sie dabei beachten, dass die Änderung 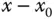 im Argument im allgemeinen Fall vektorwertig ist, da die Variablen
im Argument im allgemeinen Fall vektorwertig ist, da die Variablen 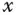 und
und 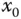 aus mehrdimensionalen Räumen stammen. Die Division durch einen Vektor ist nicht definiert, daher können Sie das Verhältnis nicht genau so als Differenzenquotienten schreiben. Mit einem kleinen technischen Trick können Sie das aber doch analog zur Situation für »eindimensionale« Funktionen definieren. Dazu stellen Sie zuerst die obige Definitionsgleichung um:
aus mehrdimensionalen Räumen stammen. Die Division durch einen Vektor ist nicht definiert, daher können Sie das Verhältnis nicht genau so als Differenzenquotienten schreiben. Mit einem kleinen technischen Trick können Sie das aber doch analog zur Situation für »eindimensionale« Funktionen definieren. Dazu stellen Sie zuerst die obige Definitionsgleichung um:
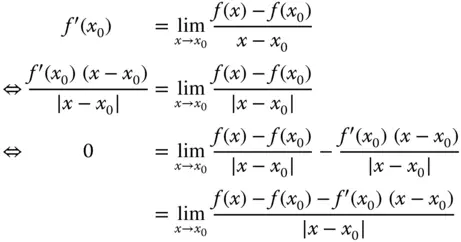
 Für einen inneren Punkt
Für einen inneren Punkt 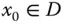 einer offenen Teilmenge
einer offenen Teilmenge 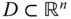 des
des 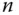 -dimensionalen Raumes
-dimensionalen Raumes 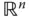 heißt eine Funktion
heißt eine Funktion 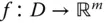 in
in 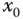 total differenzierbar , wenn es eine reelle
total differenzierbar , wenn es eine reelle  –Matrix
–Matrix 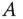 mit der Eigenschaft
mit der Eigenschaft
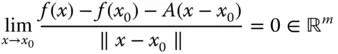
gibt. Oft sagt man statt »total differenzierbar« kurz »differenzierbar«.
Die Matrix 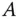 heißt 1. Ableitung oder Jacobi-Matrix der Funktion
heißt 1. Ableitung oder Jacobi-Matrix der Funktion 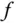 an der Stelle
an der Stelle 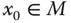 . Man bezeichnet die Matrix
. Man bezeichnet die Matrix 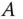 auch mit
auch mit 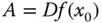 .
.
Zunächst scheint diese Definition der totalen Ableitung einer Funktion sehr formal und technisch zu sein, sie hat aber eine sehr anschauliche geometrische Bedeutung: Der Grenzwert aus der Definition der totalen Ableitung besagt nichts anderes, als dass sich die Funktionswerte 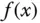 immer besser durch die Werte der affin linearen Abbildung
immer besser durch die Werte der affin linearen Abbildung 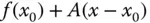 darstellen lassen, je näher
darstellen lassen, je näher 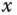 an die Stelle
an die Stelle 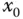 herankommt. Was das genau bedeutet und welche anderen Eigenschaften die totale Ableitung einer Funktion
herankommt. Was das genau bedeutet und welche anderen Eigenschaften die totale Ableitung einer Funktion 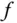 besitzt, wird im folgenden Abschnitt erläutert.
besitzt, wird im folgenden Abschnitt erläutert.
Was heißt das denn? Charakterisierungen der Differenzierbarkeit
Die meisten grundlegenden Begriffe der Analysis werden über geeignete Grenzwerte definiert. Beispiele dafür sind Stetigkeit, Ableitung und Integral einer Funktion. Solche Definitionen sind zwar aus formaler mathematischer Sicht präzise und klar, aber oft für die praktische Anwendung ziemlich unhandlich. Damit Sie Ableitungen oder Integrale tatsächlich berechnen können, braucht es zusätzliche Rechenregeln und Eigenschaften.
Im Falle der totalen Ableitung können Sie direkt aus der Grenzwertdefinition einige grundlegende Eigenschaften erkennen, die etwas mehr Licht auf die Sache werfen.
 Für eine Funktion
Für eine Funktion  und einen inneren Punkt
und einen inneren Punkt 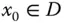 sind die folgende Aussagen äquivalent:
sind die folgende Aussagen äquivalent:
Die Funktion ist (total) differenzierbar in .
Es gilt mit .
Es gilt mit .
Die dritte Aussage ist sehr technisch und wahrscheinlich für Sie selten von Nutzen. Dagegen liefert die zweite der drei äquivalenten Aussagen die schon im vorigen Abschnitt erwähnte anschauliche geometrische Beschreibung der totalen Differenzierbarkeit und der Jacobi-Matrix von 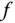 als Matrix der sich
als Matrix der sich 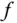 an der Stelle
an der Stelle 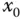 annähernden affin linearen Abbildung.
annähernden affin linearen Abbildung.
Читать дальше

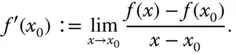
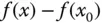 im Vergleich zur Änderung des Arguments
im Vergleich zur Änderung des Arguments 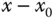 .
.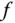 zwischen mehrdimensionalen Räumen so definiert, allerdings müssen Sie dabei beachten, dass die Änderung
zwischen mehrdimensionalen Räumen so definiert, allerdings müssen Sie dabei beachten, dass die Änderung 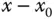 im Argument im allgemeinen Fall vektorwertig ist, da die Variablen
im Argument im allgemeinen Fall vektorwertig ist, da die Variablen 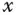 und
und 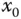 aus mehrdimensionalen Räumen stammen. Die Division durch einen Vektor ist nicht definiert, daher können Sie das Verhältnis nicht genau so als Differenzenquotienten schreiben. Mit einem kleinen technischen Trick können Sie das aber doch analog zur Situation für »eindimensionale« Funktionen definieren. Dazu stellen Sie zuerst die obige Definitionsgleichung um:
aus mehrdimensionalen Räumen stammen. Die Division durch einen Vektor ist nicht definiert, daher können Sie das Verhältnis nicht genau so als Differenzenquotienten schreiben. Mit einem kleinen technischen Trick können Sie das aber doch analog zur Situation für »eindimensionale« Funktionen definieren. Dazu stellen Sie zuerst die obige Definitionsgleichung um: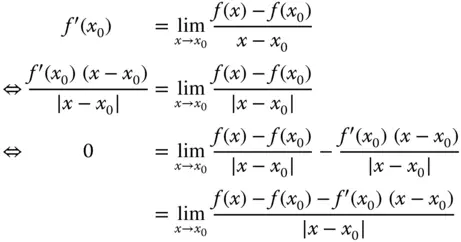
 Für einen inneren Punkt
Für einen inneren Punkt 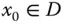 einer offenen Teilmenge
einer offenen Teilmenge 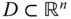 des
des 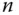 -dimensionalen Raumes
-dimensionalen Raumes 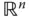 heißt eine Funktion
heißt eine Funktion 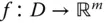 in
in 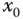 total differenzierbar , wenn es eine reelle
total differenzierbar , wenn es eine reelle  –Matrix
–Matrix 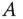 mit der Eigenschaft
mit der Eigenschaft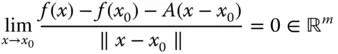
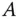 heißt 1. Ableitung oder Jacobi-Matrix der Funktion
heißt 1. Ableitung oder Jacobi-Matrix der Funktion 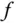 an der Stelle
an der Stelle 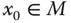 . Man bezeichnet die Matrix
. Man bezeichnet die Matrix 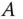 auch mit
auch mit 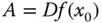 .
.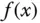 immer besser durch die Werte der affin linearen Abbildung
immer besser durch die Werte der affin linearen Abbildung 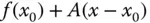 darstellen lassen, je näher
darstellen lassen, je näher 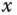 an die Stelle
an die Stelle 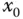 herankommt. Was das genau bedeutet und welche anderen Eigenschaften die totale Ableitung einer Funktion
herankommt. Was das genau bedeutet und welche anderen Eigenschaften die totale Ableitung einer Funktion 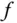 besitzt, wird im folgenden Abschnitt erläutert.
besitzt, wird im folgenden Abschnitt erläutert. Für eine Funktion
Für eine Funktion  und einen inneren Punkt
und einen inneren Punkt 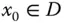 sind die folgende Aussagen äquivalent:
sind die folgende Aussagen äquivalent: als Matrix der sich
als Matrix der sich  an der Stelle
an der Stelle  annähernden affin linearen Abbildung.
annähernden affin linearen Abbildung.










