Ein Beispiel:Die Funktion 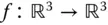 mit
mit
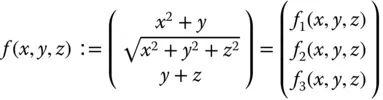
besitzt die Komponentenfunktionen  ,
, 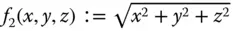 und
und 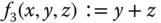 .
.
Genau wie im vorigen Abschnitt »Viele Wege führen dahin: Stetigkeit« für reellwertige Funktionen mehrerer Variablen kann Stetigkeit auch für Funktionen 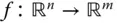 definiert werden.
definiert werden.
 Die Stetigkeitsdefinition aus dem Abschnitt »Viele Wege führen dahin: Stetigkeit« können Sie wörtlich auf Funktionen
Die Stetigkeitsdefinition aus dem Abschnitt »Viele Wege führen dahin: Stetigkeit« können Sie wörtlich auf Funktionen 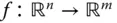 übertragen; allerdings müssen Sie dabei beachten, dass nicht nur die Punktfolgen
übertragen; allerdings müssen Sie dabei beachten, dass nicht nur die Punktfolgen 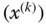 aus Punkten eines mehrdimensionalen Raumes, dem
aus Punkten eines mehrdimensionalen Raumes, dem 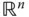 , bestehen, sondern auch die zugehörigen Folgen der Funktionswerte
, bestehen, sondern auch die zugehörigen Folgen der Funktionswerte 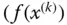 . Der Grenzwert
. Der Grenzwert
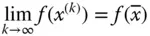
ist also ebenfalls als ein Grenzwert einer Punktfolge in einem mehrdimensionalen Raum, dem 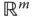 , zu verstehen.
, zu verstehen.
Ableiten bis zum Abwinken: Totale Differenzierbarkeit
Unter den wichtigen und interessanten Eigenschaften einer Funktion stehen Stetigkeit und Differenzierbarkeit an erster Stelle. Beides sind sogenannte Änderungsmodi einer Funktion. Ist eine Funktion stetig, so wissen Sie, dass eine kleine Änderung im Argument nur eine (vergleichsweise) kleine Änderung im Funktionswert zur Folge haben kann. Stetige Funktionen können nicht springen. Ist die Funktion zusätzlich differenzierbar, dann können Sie die Änderungsrate an einer bestimmten Stelle auch quantitativ angeben und erhalten dadurch die Ableitung. Anders als bei reellwertigen Funktionen einer einzigen Variablen gibt es für Funktionen zwischen mehrdimensionalen Räumen verschiedene Ableitungsbegriffe: partielle Ableitung , totale Ableitung oder Richtungsableitung . Dieser Abschnitt beschreibt diese Begriffe und liefert damit eine Einführung in die mehrdimensionale Differentialrechnung. Zunächst erkläre ich Ihnen dabei den Begriff der partiellen Ableitung für reellwertige Funktionen.
Nur einen Teil: Die partielle Ableitung
Für eine reellwertige Funktion einer einzigen Variablen ist die Ableitung in einem Punkt 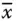 nach dem Abschnitt »Differenzierbarkeit und Kurvendiskussion« in Kapitel 1als Grenzwert des Differerenzenquotienten definiert. Anschaulich ergibt dieser Grenzwert, wenn er existiert, die Steigung der Tangenten an den Graphen der Funktion in diesem Punkt.
nach dem Abschnitt »Differenzierbarkeit und Kurvendiskussion« in Kapitel 1als Grenzwert des Differerenzenquotienten definiert. Anschaulich ergibt dieser Grenzwert, wenn er existiert, die Steigung der Tangenten an den Graphen der Funktion in diesem Punkt.
Stellen Sie sich nun eine reellwertige Funktion 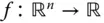 von
von 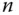 Variablen vor. Erlauben Sie bei dieser Funktion für einen Moment nur einer einzigen Variablen, zum Beispiel
Variablen vor. Erlauben Sie bei dieser Funktion für einen Moment nur einer einzigen Variablen, zum Beispiel 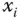 mit
mit 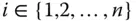 , sich tatächlich zu verändern, und halten Sie die restlichen
, sich tatächlich zu verändern, und halten Sie die restlichen 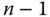 Variablen fest:
Variablen fest: 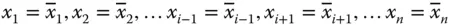 , dann erhalten Sie praktisch eine reellwertige Funktion einer einzigen Variablen:
, dann erhalten Sie praktisch eine reellwertige Funktion einer einzigen Variablen:
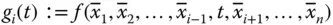
Anschaulich gesprochen stellt 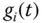 die Funktion
die Funktion 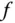 in Richtung der
in Richtung der 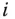 -ten Koordinate dar.
-ten Koordinate dar.
 Diese neue Funktion können Sie mit den Methoden der eindimensionalen Analysis aus dem Abschnitt »Eindimensionale Analysis« in Kapitel 1untersuchen, beispielsweise auf Differenzierbarkeit.
Diese neue Funktion können Sie mit den Methoden der eindimensionalen Analysis aus dem Abschnitt »Eindimensionale Analysis« in Kapitel 1untersuchen, beispielsweise auf Differenzierbarkeit.
Existiert der Grenzwert des Differenzenquotienten
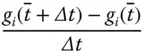
von 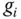 an einer Stelle
an einer Stelle 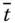 , dann ist
, dann ist 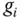 an dieser Stelle differenzierbar, und Sie erhalten mit der Ableitung von
an dieser Stelle differenzierbar, und Sie erhalten mit der Ableitung von 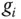 an einer Stelle
an einer Stelle 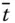 gleichzeitig die Änderungsrate der Funktion
gleichzeitig die Änderungsrate der Funktion 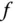 am Punkt
am Punkt 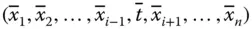 entlang der
entlang der 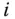 -ten Koordinatenrichtung. Diese Änderungsrate wird die
-ten Koordinatenrichtung. Diese Änderungsrate wird die 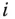 -te partielle Ableitung von
-te partielle Ableitung von 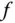 genannt.
genannt.
Читать дальше

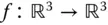 mit
mit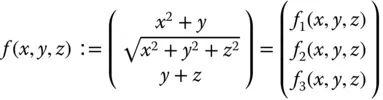
 ,
, 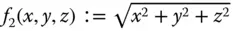 und
und 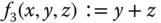 .
.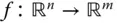 definiert werden.
definiert werden. Die Stetigkeitsdefinition aus dem Abschnitt »Viele Wege führen dahin: Stetigkeit« können Sie wörtlich auf Funktionen
Die Stetigkeitsdefinition aus dem Abschnitt »Viele Wege führen dahin: Stetigkeit« können Sie wörtlich auf Funktionen 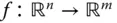 übertragen; allerdings müssen Sie dabei beachten, dass nicht nur die Punktfolgen
übertragen; allerdings müssen Sie dabei beachten, dass nicht nur die Punktfolgen 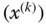 aus Punkten eines mehrdimensionalen Raumes, dem
aus Punkten eines mehrdimensionalen Raumes, dem 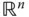 , bestehen, sondern auch die zugehörigen Folgen der Funktionswerte
, bestehen, sondern auch die zugehörigen Folgen der Funktionswerte 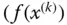 . Der Grenzwert
. Der Grenzwert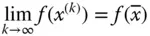
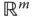 , zu verstehen.
, zu verstehen.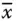 nach dem Abschnitt »Differenzierbarkeit und Kurvendiskussion« in Kapitel 1als Grenzwert des Differerenzenquotienten definiert. Anschaulich ergibt dieser Grenzwert, wenn er existiert, die Steigung der Tangenten an den Graphen der Funktion in diesem Punkt.
nach dem Abschnitt »Differenzierbarkeit und Kurvendiskussion« in Kapitel 1als Grenzwert des Differerenzenquotienten definiert. Anschaulich ergibt dieser Grenzwert, wenn er existiert, die Steigung der Tangenten an den Graphen der Funktion in diesem Punkt.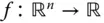 von
von 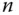 Variablen vor. Erlauben Sie bei dieser Funktion für einen Moment nur einer einzigen Variablen, zum Beispiel
Variablen vor. Erlauben Sie bei dieser Funktion für einen Moment nur einer einzigen Variablen, zum Beispiel 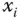 mit
mit 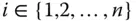 , sich tatächlich zu verändern, und halten Sie die restlichen
, sich tatächlich zu verändern, und halten Sie die restlichen 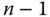 Variablen fest:
Variablen fest: 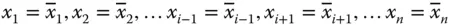 , dann erhalten Sie praktisch eine reellwertige Funktion einer einzigen Variablen:
, dann erhalten Sie praktisch eine reellwertige Funktion einer einzigen Variablen: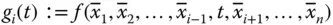
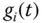 die Funktion
die Funktion 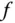 in Richtung der
in Richtung der 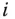 -ten Koordinate dar.
-ten Koordinate dar. Diese neue Funktion können Sie mit den Methoden der eindimensionalen Analysis aus dem Abschnitt »Eindimensionale Analysis« in Kapitel 1untersuchen, beispielsweise auf Differenzierbarkeit.
Diese neue Funktion können Sie mit den Methoden der eindimensionalen Analysis aus dem Abschnitt »Eindimensionale Analysis« in Kapitel 1untersuchen, beispielsweise auf Differenzierbarkeit.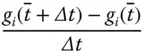
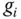 an einer Stelle
an einer Stelle 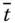 , dann ist
, dann ist 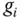 an dieser Stelle differenzierbar, und Sie erhalten mit der Ableitung von
an dieser Stelle differenzierbar, und Sie erhalten mit der Ableitung von 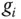 an einer Stelle
an einer Stelle 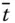 gleichzeitig die Änderungsrate der Funktion
gleichzeitig die Änderungsrate der Funktion 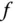 am Punkt
am Punkt 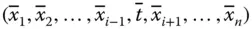 entlang der
entlang der 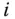 -ten Koordinatenrichtung. Diese Änderungsrate wird die
-ten Koordinatenrichtung. Diese Änderungsrate wird die 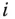 -te partielle Ableitung von
-te partielle Ableitung von 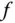 genannt.
genannt.










