Die formale Definition der partiellen Ableitung vermeidet zwar den Umweg über Hilfsfunktionen 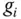 , bedeutet aber genau dasselbe.
, bedeutet aber genau dasselbe.
 Die Funktion
Die Funktion 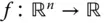 mit Definitionsbereich
mit Definitionsbereich 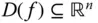 heißt im Punkt
heißt im Punkt 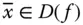 partiell nach
partiell nach 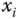 differenzierbar , falls der Grenzwert
differenzierbar , falls der Grenzwert
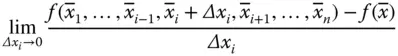
existiert.
Der Grenzwert heißt die partielle Ableitung von 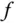 nach
nach 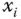 in
in  und wird mit
und wird mit
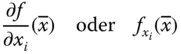
bezeichnet.
Trotzdem entspricht die partielle Ableitung von 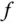 nach
nach 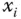 in
in 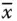 der ganz normalen »eindimensionalen« Ableitung der Funktion
der ganz normalen »eindimensionalen« Ableitung der Funktion
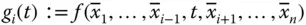
als Funktion der Variablen 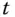 an der Stelle
an der Stelle 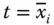 , wobei die übrigen
, wobei die übrigen  fest und damit bei der Differentiation als Konstante anzusehen sind. Es gilt:
fest und damit bei der Differentiation als Konstante anzusehen sind. Es gilt:
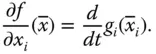
Ein Beispiel:Betrachten Sie die Funktion 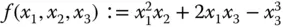 mit Definitionsbereich
mit Definitionsbereich 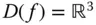 . Zur Berechnung der partiellen Ableitung
. Zur Berechnung der partiellen Ableitung 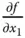 gehen Sie Schritt für Schritt so vor:
gehen Sie Schritt für Schritt so vor:
1 Setzen Sie .
2 Leiten Sie die Funktion ab.Das heißt: Berechnen Sie die Ableitung . Es gilt:
3 Sie erhalten die gesuchte partielle Ableitung, indem Sie berechnen:
Analog erhalten Sie die beiden anderen partiellen Ableitungen der Funktion 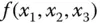 :
:
1 Setzen Sie .
2 Leiten Sie die Funktion ab.
3 Sie erhalten die gesuchte partielle Ableitung, indem Sie berechnen:
4 Setzen Sie .
5 Leiten Sie die Funktion ab.
6 Sie erhalten die gesuchte partielle Ableitung, indem Sie berechnen:
Mit ein wenig Übung werden Sie partielle Ableitungen direkt berechnen können und den Umweg über die Hilfsfunktionen 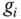 nicht mehr benötigen.
nicht mehr benötigen.
 Der Weg über die Hilfsfunktionen
Der Weg über die Hilfsfunktionen 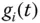 zur Berechnung partieller Ableitungen
zur Berechnung partieller Ableitungen 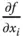 ist nicht notwendig, sondern nur eine Hilfe. Falls Sie sich sicher fühlen, dürfen Sie auch direkt »in der Funktion
ist nicht notwendig, sondern nur eine Hilfe. Falls Sie sich sicher fühlen, dürfen Sie auch direkt »in der Funktion 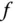 « nach der entsprechenden Variablen ableiten.
« nach der entsprechenden Variablen ableiten.
Hierzu ein Beispiel:Die Gasdruckfunktion 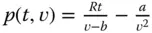 aus dem Abschnitt »Viele Variablen und ein Funktionswert« am Anfang dieses Kapitels hat die partiellen Ableitungen:
aus dem Abschnitt »Viele Variablen und ein Funktionswert« am Anfang dieses Kapitels hat die partiellen Ableitungen:
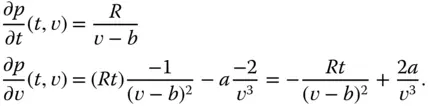
Sie sehen: Die Berechnung partieller Ableitungen ist genauso einfach, wie die Berechnung der Ableitung einer reellwertigen Funktion einer einzigen Variablen. Sie müssen dabei nur die jeweils anderen Variablen für den Moment als festgehaltene Parameter betrachten. Für eine »eindimensionale« Funktion 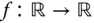 ist die partielle Ableitung
ist die partielle Ableitung
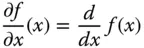
sogar genau dasselbe wie die gewöhnliche Ableitung dieser Funktion.
 Bei der Berechnung von partiellen Ableitungen dürfen Sie die Rechenregeln für gewöhnliche Ableitungen verwenden.
Bei der Berechnung von partiellen Ableitungen dürfen Sie die Rechenregeln für gewöhnliche Ableitungen verwenden.
Читать дальше

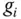 , bedeutet aber genau dasselbe.
, bedeutet aber genau dasselbe. Die Funktion
Die Funktion 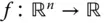 mit Definitionsbereich
mit Definitionsbereich 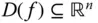 heißt im Punkt
heißt im Punkt 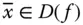 partiell nach
partiell nach 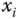 differenzierbar , falls der Grenzwert
differenzierbar , falls der Grenzwert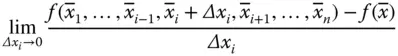
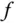 nach
nach 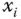 in
in  und wird mit
und wird mit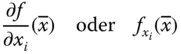
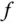 nach
nach 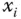 in
in 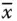 der ganz normalen »eindimensionalen« Ableitung der Funktion
der ganz normalen »eindimensionalen« Ableitung der Funktion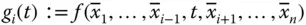
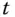 an der Stelle
an der Stelle 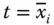 , wobei die übrigen
, wobei die übrigen  fest und damit bei der Differentiation als Konstante anzusehen sind. Es gilt:
fest und damit bei der Differentiation als Konstante anzusehen sind. Es gilt: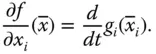
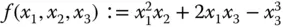 mit Definitionsbereich
mit Definitionsbereich 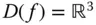 . Zur Berechnung der partiellen Ableitung
. Zur Berechnung der partiellen Ableitung 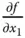 gehen Sie Schritt für Schritt so vor:
gehen Sie Schritt für Schritt so vor: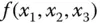 :
: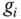 nicht mehr benötigen.
nicht mehr benötigen. Der Weg über die Hilfsfunktionen
Der Weg über die Hilfsfunktionen 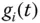 zur Berechnung partieller Ableitungen
zur Berechnung partieller Ableitungen 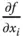 ist nicht notwendig, sondern nur eine Hilfe. Falls Sie sich sicher fühlen, dürfen Sie auch direkt »in der Funktion
ist nicht notwendig, sondern nur eine Hilfe. Falls Sie sich sicher fühlen, dürfen Sie auch direkt »in der Funktion 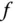 « nach der entsprechenden Variablen ableiten.
« nach der entsprechenden Variablen ableiten.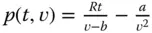 aus dem Abschnitt »Viele Variablen und ein Funktionswert« am Anfang dieses Kapitels hat die partiellen Ableitungen:
aus dem Abschnitt »Viele Variablen und ein Funktionswert« am Anfang dieses Kapitels hat die partiellen Ableitungen: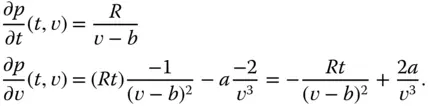
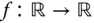 ist die partielle Ableitung
ist die partielle Ableitung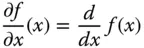
 Bei der Berechnung von partiellen Ableitungen dürfen Sie die Rechenregeln für gewöhnliche Ableitungen verwenden.
Bei der Berechnung von partiellen Ableitungen dürfen Sie die Rechenregeln für gewöhnliche Ableitungen verwenden.










