Allerdings dürfen Sie nicht alle Eigenschaften, die Sie für »eindimensionale« Funktionen automatisch aus deren Differenzierbarkeit erhalten, auch für partiell differenzierbare Funktionen 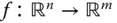 erwarten.
erwarten.
 Auch wenn die Berechnung der partiellen Ableitungen einer Funktion über die Berechnung der gewöhnlichen Ableitungen entsprechender »eindimensionaler« Funktionen erfolgt, gibt es doch deutliche Unterschiede in den Ableitungsbegriffen.
Auch wenn die Berechnung der partiellen Ableitungen einer Funktion über die Berechnung der gewöhnlichen Ableitungen entsprechender »eindimensionaler« Funktionen erfolgt, gibt es doch deutliche Unterschiede in den Ableitungsbegriffen.
Es gilt beispielsweise, dass eine an einer Stelle 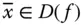 differenzierbare »eindimensionale« Funktion
differenzierbare »eindimensionale« Funktion 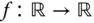 dort auch stetig sein muss. Das gilt für nur partiell differenzierbare Funktionen selbst dann nicht, wenn alle partiellen Ableitungen an einer Stelle existieren:
dort auch stetig sein muss. Das gilt für nur partiell differenzierbare Funktionen selbst dann nicht, wenn alle partiellen Ableitungen an einer Stelle existieren:
Ein Beispiel:Die Funktion
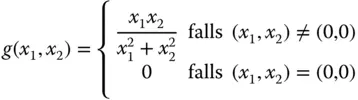
ist an der Stelle 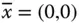 nach dem Beispiel im Abschnitt »Viele Wege führen dahin: Stetigkeit« nicht stetig. Allerdings existieren die beiden partiellen Ableitungen an dieser Stelle:
nach dem Beispiel im Abschnitt »Viele Wege führen dahin: Stetigkeit« nicht stetig. Allerdings existieren die beiden partiellen Ableitungen an dieser Stelle:
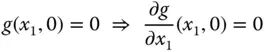
und
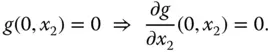
Anschaulich können Sie sich das so vorstellen, dass die Unstetigkeit von 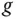 an der Stelle
an der Stelle 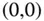 weder in der
weder in der 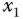 –Richtung noch in
–Richtung noch in 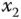 –Richtung auftritt. Eingeschränkt auf eine dieser Richtungen ist die dadurch entstehende »eindimensionale« Funktion differenzierbar und daher auch stetig. Wenn Sie sich aber wie im Abschnitt »Viele Wege führen dahin: Stetigkeit« der Stelle
–Richtung auftritt. Eingeschränkt auf eine dieser Richtungen ist die dadurch entstehende »eindimensionale« Funktion differenzierbar und daher auch stetig. Wenn Sie sich aber wie im Abschnitt »Viele Wege führen dahin: Stetigkeit« der Stelle 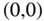 etwa aus Richtung der Winkelhalbierenden nähern, dann springt
etwa aus Richtung der Winkelhalbierenden nähern, dann springt 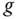 an dieser Stelle.
an dieser Stelle.
Die beiden partiellen Ableitungen enthalten also in einem gewissen Sinne zu wenig Informationen über die Funktion 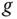 . Die Rolle der üblichen Ableitung einer »eindimensionalen« Funktion übernimmt für »mehrdimensionale« Funktionen
. Die Rolle der üblichen Ableitung einer »eindimensionalen« Funktion übernimmt für »mehrdimensionale« Funktionen 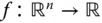 die sogenannte totale Ableitung , kurz einfach »Ableitung« genannt, die im folgenden Abschnitt behandelt wird.
die sogenannte totale Ableitung , kurz einfach »Ableitung« genannt, die im folgenden Abschnitt behandelt wird.
Partielle Ableitungen von Abbildungen zwischen mehrdimensionalen Räumen
Bislang sind in diesem Abschnitt partielle Ableitungen von reellwertigen Funktionen mehrerer Variablen betrachtet worden. Sie können den Begriff der partiellen Ableitung aber fast direkt auf Funktionen 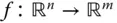 zwischen mehrdimensionalen Räumen übertragen. Eine solche vektorwertige Funktion besteht nach dem Abschnitt »Abbildungen zwischen mehrdimensionalen Räumen« aus den Komponentenfunktionen
zwischen mehrdimensionalen Räumen übertragen. Eine solche vektorwertige Funktion besteht nach dem Abschnitt »Abbildungen zwischen mehrdimensionalen Räumen« aus den Komponentenfunktionen 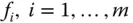 . Jede Komponentenfunktion
. Jede Komponentenfunktion 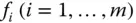 ist eine reellwertige Funktion von
ist eine reellwertige Funktion von 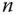 Variablen, die daher partielle Ableitungen nach den Variablen
Variablen, die daher partielle Ableitungen nach den Variablen 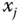 für
für 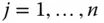 besitzen kann.
besitzen kann.
 Die partiellen Ableitungen einer Funktion
Die partiellen Ableitungen einer Funktion 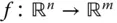 sind die partiellen Ableitungen
sind die partiellen Ableitungen 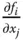 aller Komponentenfunktionen von
aller Komponentenfunktionen von 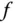 , falls diese existieren.
, falls diese existieren.
Da die partiellen Ableitungen einer Abbildung zwischen zwei mehrdimensionalen Räumen die partiellen Ableitungen ihrer Komponentenfunktionen sind, gelten die Eigenschaften und Regeln für partielle Ableitungen von reellwertigen Funktionen sinngemäß auch für die partiellen Ableitungen von vektorwertigen Funktionen.
Totale Differenzierbarkeit
Die Eigenschaft der partiellen Differenzierbarkeit ist für viele Anwendungen zu schwach. Eine stärkere Eigenschaft ist die totale Differenzierbarkeit.
Die Ableitung 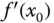 einer differenzierbaren Funktion
einer differenzierbaren Funktion 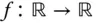 wird üblicherweise als Grenzwert des Differenzenquotienten definiert:
wird üblicherweise als Grenzwert des Differenzenquotienten definiert:
Читать дальше

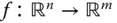 erwarten.
erwarten. Auch wenn die Berechnung der partiellen Ableitungen einer Funktion über die Berechnung der gewöhnlichen Ableitungen entsprechender »eindimensionaler« Funktionen erfolgt, gibt es doch deutliche Unterschiede in den Ableitungsbegriffen.
Auch wenn die Berechnung der partiellen Ableitungen einer Funktion über die Berechnung der gewöhnlichen Ableitungen entsprechender »eindimensionaler« Funktionen erfolgt, gibt es doch deutliche Unterschiede in den Ableitungsbegriffen.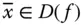 differenzierbare »eindimensionale« Funktion
differenzierbare »eindimensionale« Funktion 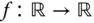 dort auch stetig sein muss. Das gilt für nur partiell differenzierbare Funktionen selbst dann nicht, wenn alle partiellen Ableitungen an einer Stelle existieren:
dort auch stetig sein muss. Das gilt für nur partiell differenzierbare Funktionen selbst dann nicht, wenn alle partiellen Ableitungen an einer Stelle existieren: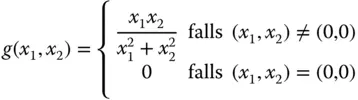
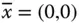 nach dem Beispiel im Abschnitt »Viele Wege führen dahin: Stetigkeit« nicht stetig. Allerdings existieren die beiden partiellen Ableitungen an dieser Stelle:
nach dem Beispiel im Abschnitt »Viele Wege führen dahin: Stetigkeit« nicht stetig. Allerdings existieren die beiden partiellen Ableitungen an dieser Stelle: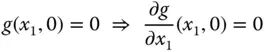
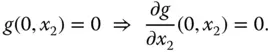
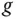 an der Stelle
an der Stelle 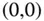 weder in der
weder in der 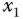 –Richtung noch in
–Richtung noch in 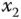 –Richtung auftritt. Eingeschränkt auf eine dieser Richtungen ist die dadurch entstehende »eindimensionale« Funktion differenzierbar und daher auch stetig. Wenn Sie sich aber wie im Abschnitt »Viele Wege führen dahin: Stetigkeit« der Stelle
–Richtung auftritt. Eingeschränkt auf eine dieser Richtungen ist die dadurch entstehende »eindimensionale« Funktion differenzierbar und daher auch stetig. Wenn Sie sich aber wie im Abschnitt »Viele Wege führen dahin: Stetigkeit« der Stelle 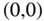 etwa aus Richtung der Winkelhalbierenden nähern, dann springt
etwa aus Richtung der Winkelhalbierenden nähern, dann springt 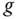 an dieser Stelle.
an dieser Stelle.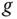 . Die Rolle der üblichen Ableitung einer »eindimensionalen« Funktion übernimmt für »mehrdimensionale« Funktionen
. Die Rolle der üblichen Ableitung einer »eindimensionalen« Funktion übernimmt für »mehrdimensionale« Funktionen 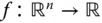 die sogenannte totale Ableitung , kurz einfach »Ableitung« genannt, die im folgenden Abschnitt behandelt wird.
die sogenannte totale Ableitung , kurz einfach »Ableitung« genannt, die im folgenden Abschnitt behandelt wird.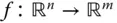 zwischen mehrdimensionalen Räumen übertragen. Eine solche vektorwertige Funktion besteht nach dem Abschnitt »Abbildungen zwischen mehrdimensionalen Räumen« aus den Komponentenfunktionen
zwischen mehrdimensionalen Räumen übertragen. Eine solche vektorwertige Funktion besteht nach dem Abschnitt »Abbildungen zwischen mehrdimensionalen Räumen« aus den Komponentenfunktionen 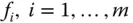 . Jede Komponentenfunktion
. Jede Komponentenfunktion 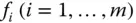 ist eine reellwertige Funktion von
ist eine reellwertige Funktion von 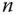 Variablen, die daher partielle Ableitungen nach den Variablen
Variablen, die daher partielle Ableitungen nach den Variablen 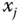 für
für 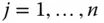 besitzen kann.
besitzen kann. Die partiellen Ableitungen einer Funktion
Die partiellen Ableitungen einer Funktion 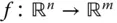 sind die partiellen Ableitungen
sind die partiellen Ableitungen 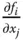 aller Komponentenfunktionen von
aller Komponentenfunktionen von 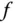 , falls diese existieren.
, falls diese existieren.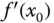 einer differenzierbaren Funktion
einer differenzierbaren Funktion 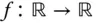 wird üblicherweise als Grenzwert des Differenzenquotienten definiert:
wird üblicherweise als Grenzwert des Differenzenquotienten definiert:










