Wie am Anfang dieses Abschnitts gesagt wurde, existieren für eine total differenzierbare Funktion 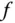 auch die partiellen Ableitungen. Die Umkehrung stimmt aber nicht immer: Eine Funktion kann an einer Stelle
auch die partiellen Ableitungen. Die Umkehrung stimmt aber nicht immer: Eine Funktion kann an einer Stelle 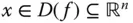 zwar alle partiellen Ableitungen besitzen, sie muss aber trotzdem nicht total differenzierbar sein.
zwar alle partiellen Ableitungen besitzen, sie muss aber trotzdem nicht total differenzierbar sein.
Ein Beispiel:Die Funktion 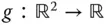 mit
mit
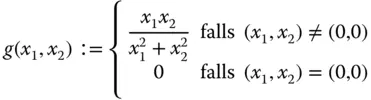
ist nach dem Abschnitt »Nur einen Teil: Die partielle Ableitung« an der Stelle 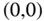 zwar nicht stetig, aber besitzt dort beide partiellen Ableitungen
zwar nicht stetig, aber besitzt dort beide partiellen Ableitungen 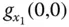 und
und 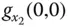 . Wäre die Funktion
. Wäre die Funktion 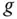 dort auch total differenzierbar, dann müsste
dort auch total differenzierbar, dann müsste 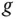 in
in 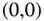 stetig sein. Da sie das nicht ist, kann sie dort nicht total differenzierbar sein.
stetig sein. Da sie das nicht ist, kann sie dort nicht total differenzierbar sein.
 Die totale Differenzierbarkeit einer Funktion bedeutet also tatsächlich mehr als die Existenz aller partiellen Ableitungen, auch wenn Sie, falls die betreffende Funktion überhaupt total differenzierbar ist, die totale Ableitung über die partiellen Ableitungen ausrechnen können.
Die totale Differenzierbarkeit einer Funktion bedeutet also tatsächlich mehr als die Existenz aller partiellen Ableitungen, auch wenn Sie, falls die betreffende Funktion überhaupt total differenzierbar ist, die totale Ableitung über die partiellen Ableitungen ausrechnen können.
Das klingt verwirrend und stellt in der Tat eine Falle dar, in die Sie bei Differenzierbarkeitsuntersuchungen geraten könnten. Allerdings können Sie den partiellen Ableitungen  oft ansehen, dass die Funktion
oft ansehen, dass die Funktion 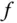 auch total differenzierbar ist.
auch total differenzierbar ist.
 Ist eine Funktion
Ist eine Funktion 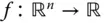 in einer Umgebung von
in einer Umgebung von 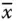 nach allen Variablen
nach allen Variablen 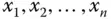 partiell differenzierbar und alle partiellen Ableitungen
partiell differenzierbar und alle partiellen Ableitungen 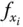 sind im Punkt
sind im Punkt 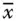 stetig, dann ist die Funktion
stetig, dann ist die Funktion 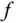 in
in 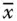 auch total differenzierbar.
auch total differenzierbar.
Für sehr viele praxisrelevante Funktionen können Sie die Stetigkeit der partiellen Ableitungen leicht feststellen und erhalten damit dann automatisch die totale Differenzierbarkeit.
Ein Beispiel:Die Funktion
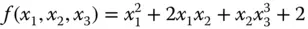
ist in der Umgebung eines jeden Punkts  partiell differenzierbar:
partiell differenzierbar:
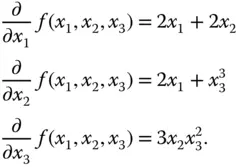
Diese partiellen Ableitungen sind Polynome in den drei Variablen 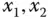 und
und 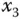 und daher überall stetig. Damit ist die Funktion
und daher überall stetig. Damit ist die Funktion 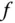 überall total differenzierbar.
überall total differenzierbar.
Wie im Abschnitt »Nur einen Teil: die partielle Ableitung« erläutert wurde, sind die partiellen Ableitungen 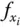 der Funktion
der Funktion 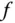 die Änderungsraten der Funktion in die Richtungen der
die Änderungsraten der Funktion in die Richtungen der 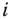 -ten Koordinatenachse. Ähnlich wie die partiellen Ableitungen in Richtung der Koordinantenachsen gibt es Richtungsableitungen einer Funktion
-ten Koordinatenachse. Ähnlich wie die partiellen Ableitungen in Richtung der Koordinantenachsen gibt es Richtungsableitungen einer Funktion 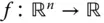 in beliebige Richtungen
in beliebige Richtungen  .
.
Für eine reellwertige Funktion können Sie sich vorstellen, dass die partiellen Ableitungen Ihnen die Steigung des Graphen in die durch die Koordinantenachsen vorgegebenen Himmelsrichtungen angibt. Eine Richtungsableitung in Richtung 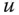 gibt Ihnen entsprechend die Steigung des Graphen in dieser Richtung an.
gibt Ihnen entsprechend die Steigung des Graphen in dieser Richtung an.
 Für eine Funktion
Für eine Funktion 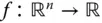 und einen Richtungsvektor
und einen Richtungsvektor  heißt
heißt
Читать дальше

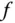 auch die partiellen Ableitungen. Die Umkehrung stimmt aber nicht immer: Eine Funktion kann an einer Stelle
auch die partiellen Ableitungen. Die Umkehrung stimmt aber nicht immer: Eine Funktion kann an einer Stelle 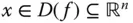 zwar alle partiellen Ableitungen besitzen, sie muss aber trotzdem nicht total differenzierbar sein.
zwar alle partiellen Ableitungen besitzen, sie muss aber trotzdem nicht total differenzierbar sein.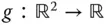 mit
mit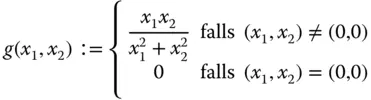
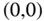 zwar nicht stetig, aber besitzt dort beide partiellen Ableitungen
zwar nicht stetig, aber besitzt dort beide partiellen Ableitungen 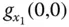 und
und 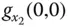 . Wäre die Funktion
. Wäre die Funktion 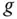 dort auch total differenzierbar, dann müsste
dort auch total differenzierbar, dann müsste 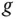 in
in 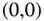 stetig sein. Da sie das nicht ist, kann sie dort nicht total differenzierbar sein.
stetig sein. Da sie das nicht ist, kann sie dort nicht total differenzierbar sein. Die totale Differenzierbarkeit einer Funktion bedeutet also tatsächlich mehr als die Existenz aller partiellen Ableitungen, auch wenn Sie, falls die betreffende Funktion überhaupt total differenzierbar ist, die totale Ableitung über die partiellen Ableitungen ausrechnen können.
Die totale Differenzierbarkeit einer Funktion bedeutet also tatsächlich mehr als die Existenz aller partiellen Ableitungen, auch wenn Sie, falls die betreffende Funktion überhaupt total differenzierbar ist, die totale Ableitung über die partiellen Ableitungen ausrechnen können. oft ansehen, dass die Funktion
oft ansehen, dass die Funktion 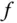 auch total differenzierbar ist.
auch total differenzierbar ist. Ist eine Funktion
Ist eine Funktion 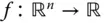 in einer Umgebung von
in einer Umgebung von 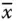 nach allen Variablen
nach allen Variablen 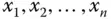 partiell differenzierbar und alle partiellen Ableitungen
partiell differenzierbar und alle partiellen Ableitungen 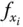 sind im Punkt
sind im Punkt 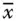 stetig, dann ist die Funktion
stetig, dann ist die Funktion 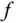 in
in 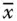 auch total differenzierbar.
auch total differenzierbar.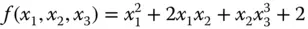
 partiell differenzierbar:
partiell differenzierbar: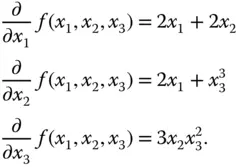
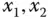 und
und 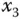 und daher überall stetig. Damit ist die Funktion
und daher überall stetig. Damit ist die Funktion 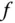 überall total differenzierbar.
überall total differenzierbar.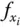 der Funktion
der Funktion 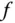 die Änderungsraten der Funktion in die Richtungen der
die Änderungsraten der Funktion in die Richtungen der 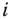 -ten Koordinatenachse. Ähnlich wie die partiellen Ableitungen in Richtung der Koordinantenachsen gibt es Richtungsableitungen einer Funktion
-ten Koordinatenachse. Ähnlich wie die partiellen Ableitungen in Richtung der Koordinantenachsen gibt es Richtungsableitungen einer Funktion 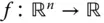 in beliebige Richtungen
in beliebige Richtungen  .
.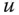 gibt Ihnen entsprechend die Steigung des Graphen in dieser Richtung an.
gibt Ihnen entsprechend die Steigung des Graphen in dieser Richtung an. Für eine Funktion
Für eine Funktion 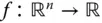 und einen Richtungsvektor
und einen Richtungsvektor  heißt
heißt










