Der Funktionswert 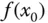 heißt lokales Maximum beziehungsweise lokales Minimum von
heißt lokales Maximum beziehungsweise lokales Minimum von 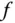 .
.
Ein 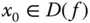 heißt lokale Extremalstelle von
heißt lokale Extremalstelle von 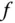 , wenn es eine lokale Minimal- oder Maximalstelle ist.
, wenn es eine lokale Minimal- oder Maximalstelle ist.
Die Bestimmung von Extremstellen beruht auf einigen grundlegenden Eigenschaften lokaler Maxima beziehungsweise lokaler Minima. Dabei reicht es zunächst, wenn Sie sich die Eigenschaften lokaler Extrema ansehen, denn jedes globale Extremum ist auch ein lokales Extremum.
 Ist die Funktion
Ist die Funktion 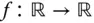 auf dem offenen Intervall
auf dem offenen Intervall 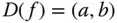 definiert und an der Stelle
definiert und an der Stelle 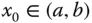 differenzierbar, dann gilt:
differenzierbar, dann gilt:
Ist 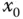 eine lokale Extremalstelle, dann ist
eine lokale Extremalstelle, dann ist 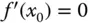 .
.
Tatsächlich muss die Ableitung nicht einmal stetig sein, es reicht schon, dass die Ableitung 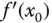 an einer Extremalstelle
an einer Extremalstelle 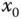 von
von 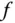 existiert. Dann muss
existiert. Dann muss 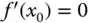 gelten.
gelten.
 Ein Punkt
Ein Punkt 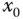 des Definitionsbereichs von
des Definitionsbereichs von 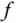 mit verschwindender Ableitung
mit verschwindender Ableitung 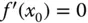 heißt ein stationärer oder kritischer Punkt .
heißt ein stationärer oder kritischer Punkt .
 Ein stationärer Punkt von
Ein stationärer Punkt von 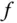 ist nicht notwendig eine Extremalstelle.
ist nicht notwendig eine Extremalstelle.
Es gilt nur: Ist 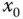 eine lokale Extremalstelle,
eine lokale Extremalstelle, 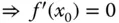 , nicht die Umkehrung.
, nicht die Umkehrung.
Außerdem kann eine Funktion eine lokale Extremstelle in einem Punkt 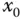 ihres Definitionsbereichs haben, ohne dort differenzierbar zu sein.
ihres Definitionsbereichs haben, ohne dort differenzierbar zu sein.
Bei der Suche nach den lokalen oder globalen Maxima und Minima einer Funktion auf einem Intervall sind die stationären Punkte mögliche Kandidaten. Da aber nicht jeder stationäre Punkt auch eine Extremstelle ist, müssen diese Punkte weiter untersucht werden.
Die zweite Ableitung ist ein Hilfsmittel, mit dem Sie an kritischen Punkten entscheiden können, ob ein Minimum oder ein Maximum vorliegt.
 Ist die Funktion
Ist die Funktion 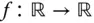 auf dem offenen Intervall
auf dem offenen Intervall 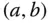 zweimal stetig differenzierbar, dann gilt für Punkte
zweimal stetig differenzierbar, dann gilt für Punkte 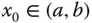 :
:
Ist und , so ist eine lokale Maximalstelle.
Ist und , so ist eine lokale Minimalstelle.
Ist 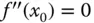 , dann können Sie nicht direkt entscheiden, ob ein Minimum, ein Maximum oder ein Sattelpunkt vorliegt.
, dann können Sie nicht direkt entscheiden, ob ein Minimum, ein Maximum oder ein Sattelpunkt vorliegt.
 Ein kritischer Punkt
Ein kritischer Punkt 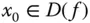 der Definitionsmenge einer differenzierbaren Funktion
der Definitionsmenge einer differenzierbaren Funktion 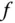 , der weder eine Minimalstelle noch eine Maximalstelle von
, der weder eine Minimalstelle noch eine Maximalstelle von 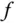 ist, heißt Sattelpunkt von
ist, heißt Sattelpunkt von 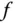 .
.
Sattelpunkte sind Spezialfälle von Wendepunkten , die gleichzeitig kritische Punkte sind. An Wendepunkten ändert sich das Krümmungsverhalten des Graphen von einer Linkskurve in eine Rechtskurve oder umgekehrt.
 Ist
Ist 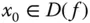 ein Punkt der Definitionsmenge einer zweimal stetig differenzierbaren Funktion
ein Punkt der Definitionsmenge einer zweimal stetig differenzierbaren Funktion 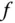 mit
mit 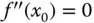 und hat die zweite Ableitung links von
und hat die zweite Ableitung links von 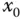 ein anderes Vorzeichen als rechts von
ein anderes Vorzeichen als rechts von 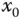 , das heißt, gilt entweder
, das heißt, gilt entweder
Читать дальше

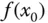 heißt lokales Maximum beziehungsweise lokales Minimum von
heißt lokales Maximum beziehungsweise lokales Minimum von 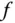 .
.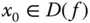 heißt lokale Extremalstelle von
heißt lokale Extremalstelle von 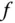 , wenn es eine lokale Minimal- oder Maximalstelle ist.
, wenn es eine lokale Minimal- oder Maximalstelle ist. Ist die Funktion
Ist die Funktion 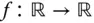 auf dem offenen Intervall
auf dem offenen Intervall 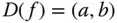 definiert und an der Stelle
definiert und an der Stelle 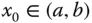 differenzierbar, dann gilt:
differenzierbar, dann gilt: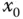 eine lokale Extremalstelle, dann ist
eine lokale Extremalstelle, dann ist 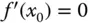 .
.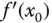 an einer Extremalstelle
an einer Extremalstelle 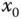 von
von 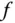 existiert. Dann muss
existiert. Dann muss 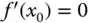 gelten.
gelten. Ein Punkt
Ein Punkt 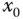 des Definitionsbereichs von
des Definitionsbereichs von 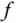 mit verschwindender Ableitung
mit verschwindender Ableitung 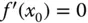 heißt ein stationärer oder kritischer Punkt .
heißt ein stationärer oder kritischer Punkt . Ein stationärer Punkt von
Ein stationärer Punkt von 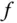 ist nicht notwendig eine Extremalstelle.
ist nicht notwendig eine Extremalstelle.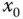 eine lokale Extremalstelle,
eine lokale Extremalstelle, 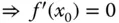 , nicht die Umkehrung.
, nicht die Umkehrung.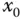 ihres Definitionsbereichs haben, ohne dort differenzierbar zu sein.
ihres Definitionsbereichs haben, ohne dort differenzierbar zu sein.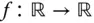 auf dem offenen Intervall
auf dem offenen Intervall 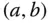 zweimal stetig differenzierbar, dann gilt für Punkte
zweimal stetig differenzierbar, dann gilt für Punkte 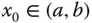 :
: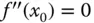 , dann können Sie nicht direkt entscheiden, ob ein Minimum, ein Maximum oder ein Sattelpunkt vorliegt.
, dann können Sie nicht direkt entscheiden, ob ein Minimum, ein Maximum oder ein Sattelpunkt vorliegt.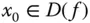 der Definitionsmenge einer differenzierbaren Funktion
der Definitionsmenge einer differenzierbaren Funktion 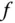 , der weder eine Minimalstelle noch eine Maximalstelle von
, der weder eine Minimalstelle noch eine Maximalstelle von 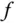 ist, heißt Sattelpunkt von
ist, heißt Sattelpunkt von 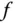 .
.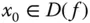 ein Punkt der Definitionsmenge einer zweimal stetig differenzierbaren Funktion
ein Punkt der Definitionsmenge einer zweimal stetig differenzierbaren Funktion 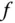 mit
mit 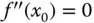 und hat die zweite Ableitung links von
und hat die zweite Ableitung links von 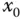 ein anderes Vorzeichen als rechts von
ein anderes Vorzeichen als rechts von 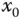 , das heißt, gilt entweder
, das heißt, gilt entweder










