 Gilt für die differenzierbaren Funktionen
Gilt für die differenzierbaren Funktionen 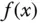 und
und 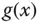 , dass das Produkt
, dass das Produkt 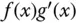 integrierbar ist, dann ist auch das Produkt
integrierbar ist, dann ist auch das Produkt 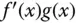 integrierbar, und es gilt die Formel:
integrierbar, und es gilt die Formel:
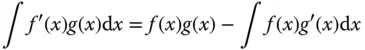
Bei der Substitution hilft die Kettenregel der Differentiation. Für die bestimmte Integration , die Flächenberechnung, müssen Sie dabei auch die Grenzen der Integrale beachten.
 Die Substitutionsformel der bestimmten Integration lautet:
Die Substitutionsformel der bestimmten Integration lautet:
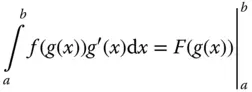
Eine zweite Form der Substitutionsregel ist ebenfalls oft nützlich.
 Eine wichtige Variante der Substitutionsformel :
Eine wichtige Variante der Substitutionsformel :
Es sei 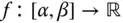 und die umkehrbare Funktion
und die umkehrbare Funktion 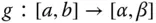 mit nicht verschwindender Ableitung
mit nicht verschwindender Ableitung 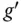 und Umkehrfunktion
und Umkehrfunktion 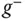 und
und 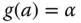 und
und 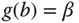 gegeben.
gegeben.
Hat 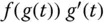 auf
auf 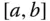 eine Stammfunktion
eine Stammfunktion 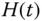 , dann ist
, dann ist 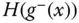 auf
auf 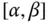 eine Stammfunktion von
eine Stammfunktion von 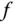 , und es gilt:
, und es gilt:
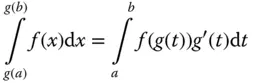
Kapitel 2
Grundlagen der Differentialrechnung im 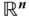
IN DIESEM KAPITEL
Funktionen mehrerer Variabler betrachten
Was Stetigkeit im Mehrdimensionalen bedeutet
Mehrdimensionale Funktionen ableiten
Höhere Ableitungen für Funktionen mehrerer Variablen bestimmen
Die mathematische Beschreibung der realen Welt ist eine wichtige Aufgabe der Naturwissenschaften und Grundlage für technische Anwendungen. Die Welt um uns herum ist offensichtlich mehrdimensional: Schon für eine einfache Ortsangabe brauchen Sie nicht nur eine einzige Variable, sondern drei Ortskoordinaten. Um naturwissenschaftliche oder technische Phänomene, wie zum Beispiel den Druck in einer dahinströmenden Flüssigkeit oder die Temperaturverteilung in einem Raum, mathematisch zu beschreiben, reichen Funktionen einer einzigen Variablen nicht aus: Nicht nur räumliche Verteilungen, sondern auch die meisten naturwissenschaftlichen Größen hängen von mehr als einem Parameter ab. Dieses Kapitel liefert eine Einführung in die Analysis zu Funktionen mehrerer Variabler.
Unsere Welt ist mehrdimensional
Genau wie bei Funktionen von einer Variablen ist für Funktionen mehrerer Variablen das Änderungsverhalten sehr interessant. Wie im eindimensionalen Fall bilden auch hierbei Grenzwertuntersuchungen die mathematische Grundlage. Allerdings sind diese im Mehrdimensionalen mitunter ein wenig trickreicher: Es gibt schon im Zweidimensionalen unendlich viele Richtungen, aus denen Sie sich einem Punkt nähern können. Dadurch entstehen unter Umständen im Mehrdimensionalen Situationen, die im Eindimensionalen nicht vorkommen können. Außerdem ist es oft viel schwieriger, sich eine Situation im Mehrdimensionalen anschaulich vorzustellen. In diesem Abschnitt erkläre ich Ihnen, was Funktionen mehrerer Veränderlicher sind, in welchen Situationen eine graphische Darstellung möglich ist und wie die analytischen Begriffe Stetigkeit und Differenzierbarkeit von Funktionen einer Variablen auf Funktionen mehrerer Variablen übertragen werden.
Viele Variablen und ein Funktionswert
Die einfachsten Beispiele für Funktionen, die von mehreren Variablen abhängen, sind lineare Abbildungen zwischen mehrdimensionalen Vektorräumen. Solche Abbildungen werden in der linearen Algebra untersucht, nachzulesen in den ersten beiden Teilen des ersten Buches »Mathematik für Ingenieure I für Dummies«. Die Analysis beschäftigt sich dagegen hauptsächlich mit nichtlinearen Abbildungen zwischen mehrdimensionalen Räumen.
Erste Beispiele dazu sind Funktionen, die mehreren Variablen eine Zahl als Funktionswert zuordnen.
Ein Beispiel:Die Van der Waalsche Zustandsgleichung für ein reales Gas beschreibt den Gasdruck in Abhängigkeit von Temperatur und Molvolumen:
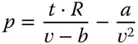
Dabei steht 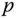 für den Gasdruck,
für den Gasdruck, 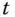 für die Temperatur und
für die Temperatur und 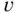 für das Molvolumen. Mit
für das Molvolumen. Mit 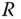 wird die allgemeine Gaskonstante bezeichnet, und
wird die allgemeine Gaskonstante bezeichnet, und 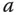 und
und 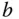 sind zwei weitere Konstanten, die je nach dem betrachteten speziellen Gas gewählt werden müssen.
sind zwei weitere Konstanten, die je nach dem betrachteten speziellen Gas gewählt werden müssen.
Читать дальше

 Gilt für die differenzierbaren Funktionen
Gilt für die differenzierbaren Funktionen 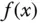 und
und 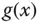 , dass das Produkt
, dass das Produkt 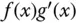 integrierbar ist, dann ist auch das Produkt
integrierbar ist, dann ist auch das Produkt 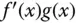 integrierbar, und es gilt die Formel:
integrierbar, und es gilt die Formel: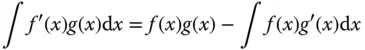
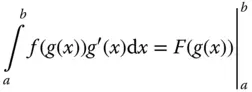
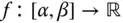 und die umkehrbare Funktion
und die umkehrbare Funktion 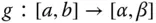 mit nicht verschwindender Ableitung
mit nicht verschwindender Ableitung 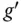 und Umkehrfunktion
und Umkehrfunktion 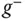 und
und 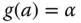 und
und 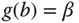 gegeben.
gegeben.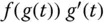 auf
auf 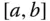 eine Stammfunktion
eine Stammfunktion 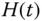 , dann ist
, dann ist 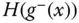 auf
auf 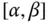 eine Stammfunktion von
eine Stammfunktion von 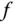 , und es gilt:
, und es gilt: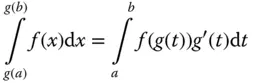
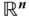
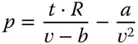
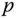 für den Gasdruck,
für den Gasdruck, 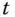 für die Temperatur und
für die Temperatur und 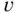 für das Molvolumen. Mit
für das Molvolumen. Mit 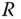 wird die allgemeine Gaskonstante bezeichnet, und
wird die allgemeine Gaskonstante bezeichnet, und 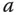 und
und 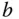 sind zwei weitere Konstanten, die je nach dem betrachteten speziellen Gas gewählt werden müssen.
sind zwei weitere Konstanten, die je nach dem betrachteten speziellen Gas gewählt werden müssen.










