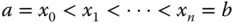
ist eine Summe
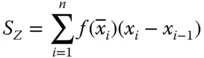
mit Zwischenpunkten 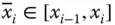 . Eine solche Unterteilung des Intervalls
. Eine solche Unterteilung des Intervalls 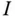 in lauter Teilintervalle
in lauter Teilintervalle 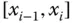 wird Zerlegung von
wird Zerlegung von 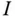 genannt. Die Feinheit einer Zerlegung ist die maximale Länge
genannt. Die Feinheit einer Zerlegung ist die maximale Länge 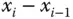 eines Teilintervalls der Zerlegung.
eines Teilintervalls der Zerlegung.
Eine Riemannsche Summe ist also nichts anderes als eine Näherung an die Fläche unter dem Graphen von 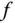 durch viele kleine Rechtecke der Breite
durch viele kleine Rechtecke der Breite 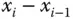 und Höhe
und Höhe 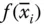 , wie Sie in Abbildung 1.5dargestellt ist.
, wie Sie in Abbildung 1.5dargestellt ist.
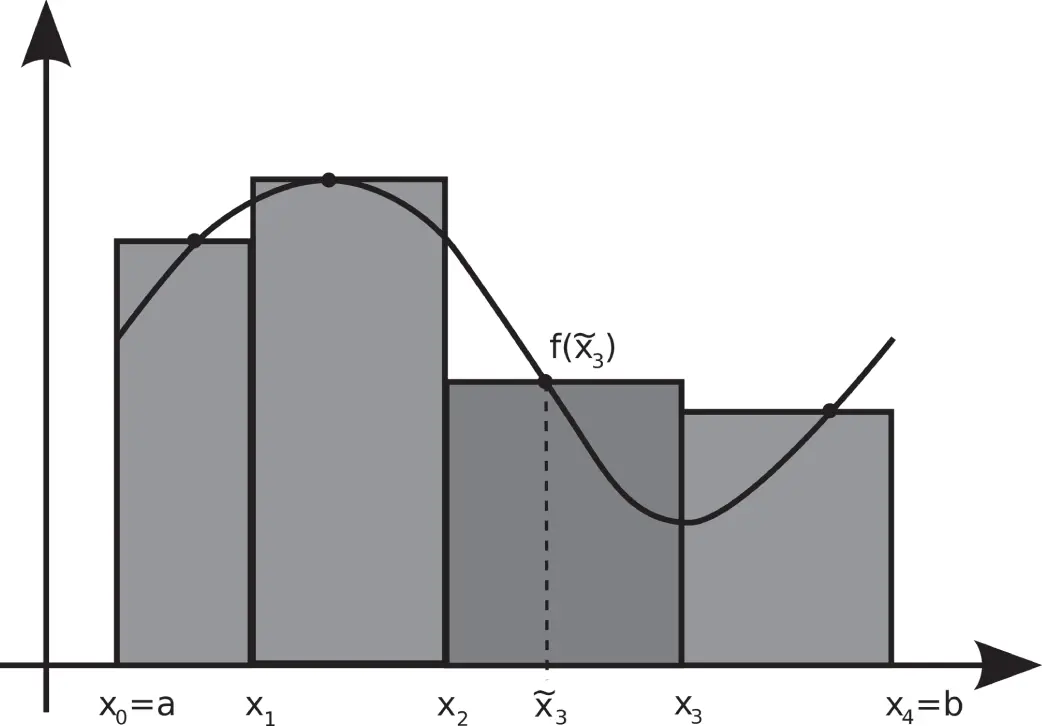
Abbildung 1.5: Approximation der Fläche 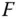 durch Rechtecksflächen
durch Rechtecksflächen
Falls alle möglichen Riemannschen Summen für immer kleinere Feinheiten der zugrunde liegenden Zerlegung gegen ein und denselben festen Wert konvergieren, dann erhalten Sie damit das Integral der Funktion 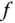 .
.
 Es sei
Es sei 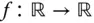 eine auf dem Intervall
eine auf dem Intervall 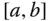 beschränkte Funktion mit
beschränkte Funktion mit 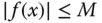 für alle
für alle 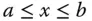 .
.
Konvergieren für alle Folgen von Zerlegungen 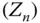 mit
mit 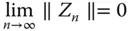 und eine beliebige Auswahl von Zwischenpunkten die Riemannschen Summen
und eine beliebige Auswahl von Zwischenpunkten die Riemannschen Summen 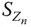 gegen einen gemeinsamen Grenzwert
gegen einen gemeinsamen Grenzwert 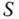 , dann heißt
, dann heißt 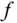 integrierbar auf [a,b] , und die Zahl
integrierbar auf [a,b] , und die Zahl 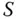 heißt bestimmtes Integral über
heißt bestimmtes Integral über 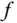 im Intervall [a,b] . In Formeln:
im Intervall [a,b] . In Formeln:
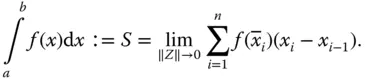
Überraschend ist der Zusammenhang zwischen der Differentialrechnung und der zunächst rein geometrisch definierten Integralrechnung. Sie erhalten mit der Flächenberechnung gleichzeitig eine Umkehrung der Differentiation.
Diese Tatsache heißt in der reellen Analysis der Hauptsatz der Differential- und Integralrechnung .
 Der Hauptsatz der Differential- und Integralrechnung erlaubt Ihnen, Integrale mit Hilfe von Stammfunktionen und umgekehrt Stammfunktionen durch Integrale zu berechnen:
Der Hauptsatz der Differential- und Integralrechnung erlaubt Ihnen, Integrale mit Hilfe von Stammfunktionen und umgekehrt Stammfunktionen durch Integrale zu berechnen:
Für jede auf einem Intervall 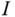 stetige Funktion
stetige Funktion 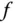 und jedes
und jedes 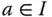 gilt:
gilt:
Existenz von Stammfunktionen: Die Funktionmit ist eine Stammfunktion zu auf .
Eindeutigkeit: Jede andere Stammfunktion zu hat die Form mit einer Konstanten .
Integralberechnung: Ist eine beliebige Stammfunktion zu , so gilt für :
Mit dem Hauptsatz der Differential- und Integralrechnung haben Sie also eine Methode, um entweder Flächen unterhalb des Graphen einer gegebenen Funktion 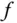 oder Stammfunktionen von
oder Stammfunktionen von 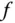 zu bestimmen, vorausgesetzt, Sie können das Integral über die Funktion
zu bestimmen, vorausgesetzt, Sie können das Integral über die Funktion 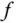 berechnen.
berechnen.
Anstatt die Grenzwertdefinition des Integrals direkt zu verwenden, werden Sie üblicherweise zur Integration einer gegebenen Funktion 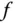 eine andere Integrationsmethode verwenden. Die beiden wichtigsten Methoden zur Integration sind die partielle Integration und die Substitutionsformel .
eine andere Integrationsmethode verwenden. Die beiden wichtigsten Methoden zur Integration sind die partielle Integration und die Substitutionsformel .
Die partielle Integration wird aus der Produktregel der Differentiation abgeleitet.
Читать дальше

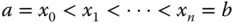
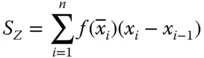
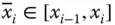 . Eine solche Unterteilung des Intervalls
. Eine solche Unterteilung des Intervalls 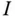 in lauter Teilintervalle
in lauter Teilintervalle 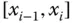 wird Zerlegung von
wird Zerlegung von 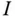 genannt. Die Feinheit einer Zerlegung ist die maximale Länge
genannt. Die Feinheit einer Zerlegung ist die maximale Länge 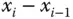 eines Teilintervalls der Zerlegung.
eines Teilintervalls der Zerlegung.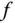 durch viele kleine Rechtecke der Breite
durch viele kleine Rechtecke der Breite 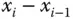 und Höhe
und Höhe 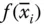 , wie Sie in Abbildung 1.5dargestellt ist.
, wie Sie in Abbildung 1.5dargestellt ist.
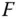 durch Rechtecksflächen
durch Rechtecksflächen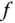 .
. Es sei
Es sei 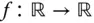 eine auf dem Intervall
eine auf dem Intervall 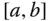 beschränkte Funktion mit
beschränkte Funktion mit 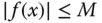 für alle
für alle 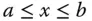 .
.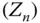 mit
mit 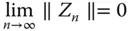 und eine beliebige Auswahl von Zwischenpunkten die Riemannschen Summen
und eine beliebige Auswahl von Zwischenpunkten die Riemannschen Summen 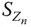 gegen einen gemeinsamen Grenzwert
gegen einen gemeinsamen Grenzwert 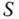 , dann heißt
, dann heißt 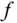 integrierbar auf [a,b] , und die Zahl
integrierbar auf [a,b] , und die Zahl 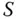 heißt bestimmtes Integral über
heißt bestimmtes Integral über 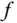 im Intervall [a,b] . In Formeln:
im Intervall [a,b] . In Formeln: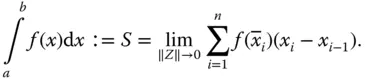
 Der Hauptsatz der Differential- und Integralrechnung erlaubt Ihnen, Integrale mit Hilfe von Stammfunktionen und umgekehrt Stammfunktionen durch Integrale zu berechnen:
Der Hauptsatz der Differential- und Integralrechnung erlaubt Ihnen, Integrale mit Hilfe von Stammfunktionen und umgekehrt Stammfunktionen durch Integrale zu berechnen: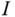 stetige Funktion
stetige Funktion 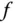 und jedes
und jedes 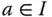 gilt:
gilt: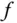 oder Stammfunktionen von
oder Stammfunktionen von 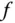 zu bestimmen, vorausgesetzt, Sie können das Integral über die Funktion
zu bestimmen, vorausgesetzt, Sie können das Integral über die Funktion 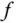 berechnen.
berechnen.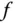 eine andere Integrationsmethode verwenden. Die beiden wichtigsten Methoden zur Integration sind die partielle Integration und die Substitutionsformel .
eine andere Integrationsmethode verwenden. Die beiden wichtigsten Methoden zur Integration sind die partielle Integration und die Substitutionsformel .










