J. Michael Fried - Mathematik für Ingenieure II für Dummies
Здесь есть возможность читать онлайн «J. Michael Fried - Mathematik für Ingenieure II für Dummies» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на немецком языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Mathematik für Ingenieure II für Dummies
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:5 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Mathematik für Ingenieure II für Dummies: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Mathematik für Ingenieure II für Dummies»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.

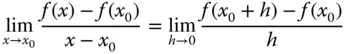
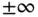 ist.
ist.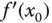 bezeichnet und heißt die Ableitung der Funktion
bezeichnet und heißt die Ableitung der Funktion 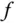 an der Stelle
an der Stelle 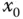 .
.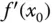 ist der Differentialquotient :
ist der Differentialquotient :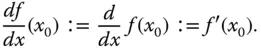
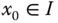 eine Ableitung, manche Funktionen sind sogar nirgends differenzierbar. Andere Funktionen sind dagegen auf ihrem ganzen Definitionsbereich differenzierbar und definieren damit eine weitere Funktion.
eine Ableitung, manche Funktionen sind sogar nirgends differenzierbar. Andere Funktionen sind dagegen auf ihrem ganzen Definitionsbereich differenzierbar und definieren damit eine weitere Funktion. Eine Funktion
Eine Funktion 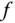 heißt auf
heißt auf 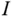 differenzierbar, falls
differenzierbar, falls 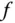 an jeder Stelle
an jeder Stelle 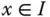 differenzierbar ist. Die Funktion
differenzierbar ist. Die Funktion 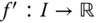 mit
mit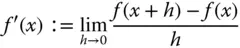
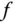 .
.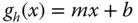 durch die beiden Punkte
durch die beiden Punkte 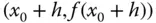 und
und 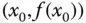 .
.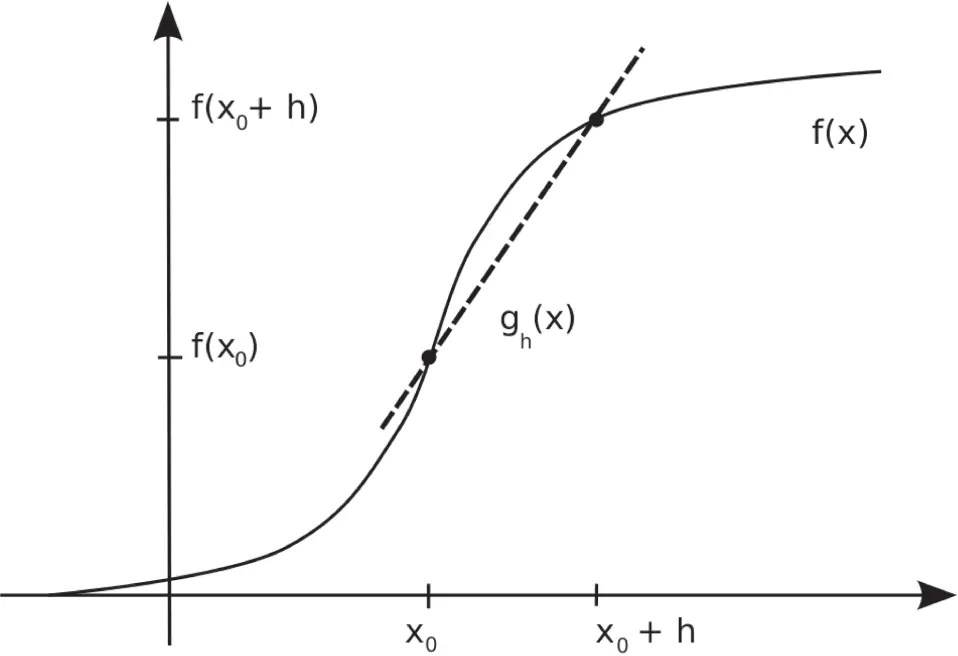
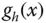 durch die beiden Punkte
durch die beiden Punkte 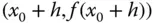 und
und 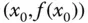
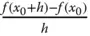 entspricht gerade der Steigung der Geraden
entspricht gerade der Steigung der Geraden 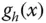 . Wenn Sie den Grenzübergang
. Wenn Sie den Grenzübergang 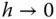 durchführen, erhalten Sie die Gerade
durchführen, erhalten Sie die Gerade 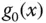 mit:
mit: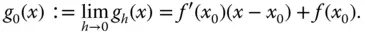
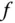 an der Stelle
an der Stelle 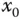 .
. Die Ableitung
Die Ableitung 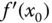 entspricht also der Steigung der Tangente an den Graphen der Funktion
entspricht also der Steigung der Tangente an den Graphen der Funktion 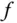 im Punkt
im Punkt 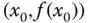 und wird daher auch Steigung der Funktion
und wird daher auch Steigung der Funktion 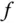 an der Stelle
an der Stelle 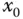 genannt.
genannt.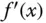 fragen, ob diese wieder differenzierbar ist. Und falls dies so ist, auch für die Ableitung der Ableitung und so weiter. Das rechtfertigt die folgende Definition der n-ten Ableitung .
fragen, ob diese wieder differenzierbar ist. Und falls dies so ist, auch für die Ableitung der Ableitung und so weiter. Das rechtfertigt die folgende Definition der n-ten Ableitung .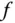 und die entsprechenden Ableitungsfunktionen von
und die entsprechenden Ableitungsfunktionen von 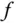 jeweils differenzierbar sind, bezeichnet man:
jeweils differenzierbar sind, bezeichnet man:










