Daniel J. Duffy - Numerical Methods in Computational Finance
Здесь есть возможность читать онлайн «Daniel J. Duffy - Numerical Methods in Computational Finance» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Numerical Methods in Computational Finance
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:4 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Numerical Methods in Computational Finance: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Numerical Methods in Computational Finance»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
Part A Mathematical Foundation for One-Factor Problems
Chapters 1 to 7 introduce the mathematical and numerical analysis concepts that are needed to understand the finite difference method and its application to computational finance.
Part B Mathematical Foundation for Two-Factor Problems
Chapters 8 to 13 discuss a number of rigorous mathematical techniques relating to elliptic and parabolic partial differential equations in two space variables. In particular, we develop strategies to preprocess and modify a PDE before we approximate it by the finite difference method, thus avoiding ad-hoc and heuristic tricks.
Part C The Foundations of the Finite Difference Method (FDM)
Chapters 14 to 17 introduce the mathematical background to the finite difference method for initial boundary value problems for parabolic PDEs. It encapsulates all the background information to construct stable and accurate finite difference schemes.
Part D Advanced Finite Difference Schemes for Two-Factor Problems
Chapters 18 to 22 introduce a number of modern finite difference methods to approximate the solution of two factor partial differential equations. This is the only book we know of that discusses these methods in any detail.
Part E Test Cases in Computational Finance
Chapters 23 to 26 are concerned with applications based on previous chapters. We discuss finite difference schemes for a wide range of one-factor and two-factor problems.
This book is suitable as an entry-level introduction as well as a detailed treatment of modern methods as used by industry quants and MSc/MFE students in finance. The topics have applications to numerical analysis, science and engineering.
More on computational finance and the author’s online courses, see www.datasim.nl.

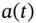 and
and 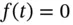 . We wish to produce a difference scheme in such a way that the discrete solution is equal to the exact solution at the mesh points for this constant-coefficient case. We introduce a so-called fitting factor
. We wish to produce a difference scheme in such a way that the discrete solution is equal to the exact solution at the mesh points for this constant-coefficient case. We introduce a so-called fitting factor 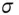 in the new scheme:
in the new scheme: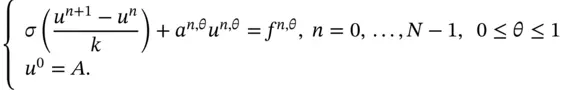
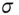 :
: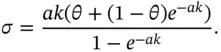
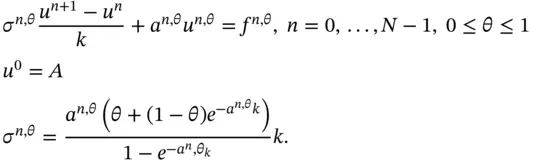

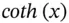 is the hyperbolic cotangent function.
is the hyperbolic cotangent function.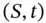 space where
space where 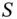 is the underlying asset and
is the underlying asset and 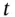 is time (up to maturity
is time (up to maturity 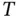 ). This is in contrast to the Crank–Nicolson scheme where the spurious oscillations are seen, especially when the underlying
). This is in contrast to the Crank–Nicolson scheme where the spurious oscillations are seen, especially when the underlying 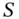 is near the strike price
is near the strike price 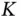 or when the payoff function is discontinuous.
or when the payoff function is discontinuous.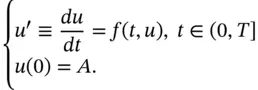
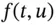 is a non-linear function in u in general. Of course, Equation (2.28)contains Equation (2.1)as a special case. However, it is not possible to come up with an exact solution for (2.28)in general, and we must resort to some numerical techniques. Approximating (2.28)poses challenges because the resulting difference schemes may also be non-linear, thus forcing us to solve the discrete system at each time level by Newton's method or some other non-linear solver. For example, consider applying the trapezoidal method to (2.28):
is a non-linear function in u in general. Of course, Equation (2.28)contains Equation (2.1)as a special case. However, it is not possible to come up with an exact solution for (2.28)in general, and we must resort to some numerical techniques. Approximating (2.28)poses challenges because the resulting difference schemes may also be non-linear, thus forcing us to solve the discrete system at each time level by Newton's method or some other non-linear solver. For example, consider applying the trapezoidal method to (2.28):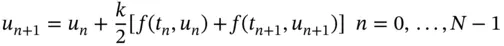
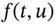 is non-linear. Here see that the unknown term u is on both the left- and right-hand sides of the equation, and hence it is not possible to solve the problem explicitly in the way that we did for the linear case. However, not all is lost, and to this end we introduce the predictor-corrector method that consists of a set consisting of two difference schemes; the first equation uses the explicit Euler method to produce an intermediate solution called a predictor that is then used in what could be called a modified trapezoidal rule :
is non-linear. Here see that the unknown term u is on both the left- and right-hand sides of the equation, and hence it is not possible to solve the problem explicitly in the way that we did for the linear case. However, not all is lost, and to this end we introduce the predictor-corrector method that consists of a set consisting of two difference schemes; the first equation uses the explicit Euler method to produce an intermediate solution called a predictor that is then used in what could be called a modified trapezoidal rule :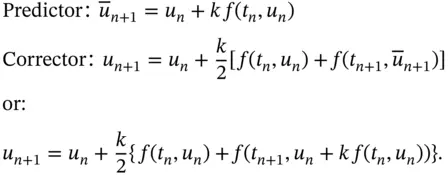
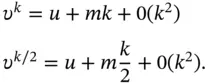
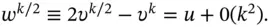
 is a second-order approximation to the solution of (2.1).
is a second-order approximation to the solution of (2.1).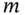 is independent of
is independent of 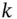 , and this is why we can eliminate it in the first equations to get a scheme that is second-order accurate. The same trick can be employed with the second-order Crank–Nicolson scheme to get a fourth-order accurate scheme as follows:
, and this is why we can eliminate it in the first equations to get a scheme that is second-order accurate. The same trick can be employed with the second-order Crank–Nicolson scheme to get a fourth-order accurate scheme as follows: