1 Cover
2 Title Page Solutions Manual to Accompany An Introduction to Numerical Methods and Analysis THIRD EDITION James F. Epperson Mathematical Reviews, American Mathematical Society
3 Copyright
4 Preface to the Solutions Manual for the Third Edition
5 CHAPTER 1: INTRODUCTORY CONCEPTS AND CALCULUS REVIEW1.1 BASIC TOOLS OF CALCULUS 1.2 ERROR, APPROXIMATE EQUALITY, AND ASYMPTOTIC ORDER NOTATION 1.3 A PRIMER ON COMPUTER ARITHMETIC 1.4 A WORD ON COMPUTER LANGUAGES AND SOFTWARE 1.5 A BRIEF HISTORY OF SCIENTIFIC COMPUTING
6 Chapter 2: A SURVEY OF SIMPLE METHODS AND TOOLS2.1 HORNER'S RULE AND NESTED MULTIPLICATION 2.2 DIFFERENCE APPROXIMATIONS TO THE DERIVATIVE 2.3 APPLICATION: EULER'S METHOD FOR INITIAL VALUE PROBLEMS 2.4 LINEAR INTERPOLATION 2.5 APPLICATION — THE TRAPEZOID RULE 2.6 SOLUTION OF TRIDIAGONAL LINEAR SYSTEMS 2.7 APPLICATION: SIMPLE TWO‐POINT BOUNDARY VALUE PROBLEMS
7 CHAPTER 3: ROOT‐FINDING 3.1 THE BISECTION METHOD 3.2 NEWTON'S METHOD: DERIVATION AND EXAMPLES 3.3 HOW TO STOP NEWTON'S METHOD 3.4 APPLICATION: DIVISION USING NEWTON'S METHOD 3.5 THE NEWTON ERROR FORMULA 3.6 NEWTON'S METHOD: THEORY AND CONVERGENCE 3.7 APPLICATION: COMPUTATION OF THE SQUARE ROOT 3.8 THE SECANT METHOD: DERIVATION AND EXAMPLES 3.9 FIXED POINT ITERATION 3.10 ROOTS OF POLYNOMIALS (PART 1) 3.11 SPECIAL TOPICS IN ROOT‐FINDING METHODS 3.12 VERY HIGH‐ORDER METHODS AND THE EFFICIENCY INDEX NOTES
8 CHAPTER 4: INTERPOLATION AND APPROXIMATION4.1 LAGRANGE INTERPOLATION 4.2 NEWTON INTERPOLATION AND DIVIDED DIFFERENCES 4.3 INTERPOLATION ERROR 4.4 APPLICATION: MULLER'S METHOD AND INVERSE QUADRATIC INTERPOLATION 4.5 APPLICATION: MORE APPROXIMATIONS TO THE DERIVATIVE 4.6 HERMITE INTERPOLATION 4.7 PIECEWISE POLYNOMIAL INTERPOLATION 4.8 AN INTRODUCTION TO SPLINES 4.9 TENSION SPLINES 4.10 LEAST SQUARES CONCEPTS IN APPROXIMATION 4.11 ADVANCED TOPICS IN INTERPOLATION ERROR NOTES
9 CHAPTER 5: NUMERICAL INTEGRATION5.1 A REVIEW OF THE DEFINITE INTEGRAL 5.2 IMPROVING THE TRAPEZOID RULE 5.3 SIMPSON'S RULE AND DEGREE OF PRECISION 5.4 THE MIDPOINT RULE 5.5 APPLICATION: STIRLING'S FORMULA 5.6 GAUSSIAN QUADRATURE 5.7 EXTRAPOLATION METHODS 5.8 SPECIAL TOPICS IN NUMERICAL INTEGRATION
10 CHAPTER 6: NUMERICAL METHODS FOR ORDINARY DIFFERENTIAL EQUATIONS6.1 The Initial Value Problem—Background 6.2 Euler's Method 6.3 Analysis of Euler's Method 6.4 Variants of Euler's Method 6.5 Single Step Methods—Runge‐Kutta 6.6 Multistep Methods 6.7 Stability Issues 6.8 Application to Systems of Equations 6.9 Adaptive Solvers 6.10 Boundary Value Problems NOTE
11 CHAPTER 7: NUMERICAL METHODS FOR THE SOLUTION OF SYSTEMS OF EQUATIONS7.1 LINEAR ALGEBRA REVIEW 7.2 LINEAR SYSTEMS AND GAUSSIAN ELIMINATION 7.3 OPERATION COUNTS 7.4 THE FACTORIZATION 7.5 PERTURBATION, CONDITIONING AND STABILITY 7.6 SPD MATRICES AND THE CHOLESKY DECOMPOSITION 7.7 APPLICATION: NUMERICAL SOLUTION OF LINEAR LEAST SQUARES PROBLEMS 7.8 SPARSE AND STRUCTURED MATRICES 7.9 ITERATIVE METHODS FOR LINEAR SYSTEMS – A BRIEF SURVEY 7.10 NONLINEAR SYSTEMS: NEWTON'S METHOD AND RELATED IDEAS 7.11 APPLICATION: NUMERICAL SOLUTION OF NONLINEAR BVP's
12 CHAPTER 8: APPROXIMATE SOLUTION OF THE ALGEBRAIC EIGENVALUE PROBLEM8.1 EIGENVALUE REVIEW 8.2 REDUCTION TO HESSENBERG FORM 8.3 POWER METHODS 8.4 BISECTION AND INERTIA TO COMPUTE EIGENVALUES OF SYMMETRIC MATRICES 8.5 AN OVERVIEW OF THE ITERATION 8.6 APPLICATION: ROOTS OF POLYNOMIALS, II 8.7 APPLICATION: COMPUTATION OF GAUSSIAN QUADRATURE RULES NOTE
13 CHAPTER 9: A SURVEY OF NUMERICAL METHODS FOR PARTIAL DIFFERENTIAL EQUATIONS9.1 DIFFERENCE METHODS FOR THE DIFFUSION EQUATION 9.2 FINITE ELEMENT METHODS FOR THE DIFFUSION EQUATION 9.3 DIFFERENCE METHODS FOR POISSON EQUATIONS NOTE
14 CHAPTER 10: AN INTRODUCTION TO SPECTRAL METHODS10.1 SPECTRAL METHODS FOR TWO‐POINT BOUNDARY VALUE PROBLEMS 10.2 SPECTRAL METHODS IN TWO DIMENSIONS 10.3 SPECTRAL METHODS FOR TIME‐DEPENDENT PROBLEMS 10.4 CLENSHAW‐CURTIS QUADRATURE
15 End User License Agreement
1 Chapter 2 Table 2.1 Derivative Approximations. Table 2.2 Table for Problem 4. Table 2.3 (Table 2.1 in text.) Example of derivative approximation to 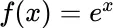 at
at 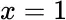 .... Table 2.4 Solution values for Exercise 2.3.11. Table 2.5 (Table 2.8 in the text) Table of
.... Table 2.4 Solution values for Exercise 2.3.11. Table 2.5 (Table 2.8 in the text) Table of 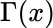 values.
values.
2 Chapter 3Table 3.1 Solutions to Problem 3.1.3Table 3.2 Solutions to Problem 3.1.10.Table 3.3 Solution to Problem 3.2.11.Table 3.4 Solutions to Problem 3.3.3.Table 3.5 Newton iteration for Problem 4d, §3.4.Table 3.6 Data for Problems 3 and 4.Table 3.7 Newton iteration for 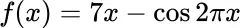 .Table 3.8 Secant iteration for
.Table 3.8 Secant iteration for 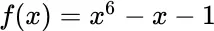 .Table 3.9 Solutions to Problem 3.10.6.Table 3.10 Solutions to Problem 3.10.7.Table 3.11 Solutions to Problem 3.10.8.Table 3.12 Hybrid iteration for
.Table 3.9 Solutions to Problem 3.10.6.Table 3.10 Solutions to Problem 3.10.7.Table 3.11 Solutions to Problem 3.10.8.Table 3.12 Hybrid iteration for 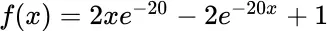 .Table 3.13 Regula‐falsi iteration for
.Table 3.13 Regula‐falsi iteration for 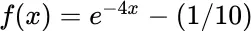 .Table 3.14 Hybrid iteration for
.Table 3.14 Hybrid iteration for 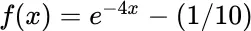 .
.
3 Chapter 4Table 4.1 Data for Problem 7.Table 4.2 Data for Problem 8.Table 4.3 Table of 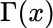 values.Table 4.4 Table of
values.Table 4.4 Table of 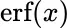 values for Problem 10.Table 4.5 Temperature‐pressure values for steam; Problem 11.Table 4.6 Temperature‐pressure values for gaseous ammonia; Problem 12.Table 4.7 Data for Problem 13.Table 4.8 Solutions to Exercise 4.4.9Table 4.9 Table for divided differences for quintic Hermite interpolation.Table 4.10 Divided difference table.Table 4.11 Data for Problem 13.Table 4.12 Data for Problem 21.Table 4.13 Data for Problem 2.Table 4.14 Data for Problem 4.Table 4.15 Data for Problem 5.Table 4.16 Data for Problem 6.Table 4.17 Data for Problem 7.
values for Problem 10.Table 4.5 Temperature‐pressure values for steam; Problem 11.Table 4.6 Temperature‐pressure values for gaseous ammonia; Problem 12.Table 4.7 Data for Problem 13.Table 4.8 Solutions to Exercise 4.4.9Table 4.9 Table for divided differences for quintic Hermite interpolation.Table 4.10 Divided difference table.Table 4.11 Data for Problem 13.Table 4.12 Data for Problem 21.Table 4.13 Data for Problem 2.Table 4.14 Data for Problem 4.Table 4.15 Data for Problem 5.Table 4.16 Data for Problem 6.Table 4.17 Data for Problem 7.
4 Chapter 5Table 5.1 Data for Problem 6.Table 5.2 Results for Exercise 5.3.6.Table 5.3 Results for Exercise 5.4.7.Table 5.4 Data for Problem 10.Table 5.5 Table of 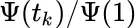 for
for 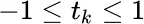 .
.
5 Chapter 6Table 6.1 Solutions to Exercise 6.2.4.Table 6.2 Results for Problem 8, first part.Table 6.3 Results for Problem 8, second part.
Читать дальше

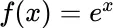 at
at 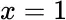 .... Table 2.4 Solution values for Exercise 2.3.11. Table 2.5 (Table 2.8 in the text) Table of
.... Table 2.4 Solution values for Exercise 2.3.11. Table 2.5 (Table 2.8 in the text) Table of  values.
values.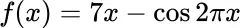 .Table 3.8 Secant iteration for
.Table 3.8 Secant iteration for 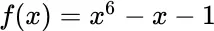 .Table 3.9 Solutions to Problem 3.10.6.Table 3.10 Solutions to Problem 3.10.7.Table 3.11 Solutions to Problem 3.10.8.Table 3.12 Hybrid iteration for
.Table 3.9 Solutions to Problem 3.10.6.Table 3.10 Solutions to Problem 3.10.7.Table 3.11 Solutions to Problem 3.10.8.Table 3.12 Hybrid iteration for 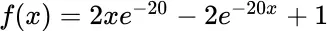 .Table 3.13 Regula‐falsi iteration for
.Table 3.13 Regula‐falsi iteration for 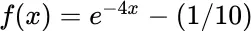 .Table 3.14 Hybrid iteration for
.Table 3.14 Hybrid iteration for 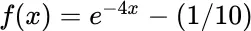 .
.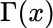 values.Table 4.4 Table of
values.Table 4.4 Table of 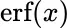 values for Problem 10.Table 4.5 Temperature‐pressure values for steam; Problem 11.Table 4.6 Temperature‐pressure values for gaseous ammonia; Problem 12.Table 4.7 Data for Problem 13.Table 4.8 Solutions to Exercise 4.4.9Table 4.9 Table for divided differences for quintic Hermite interpolation.Table 4.10 Divided difference table.Table 4.11 Data for Problem 13.Table 4.12 Data for Problem 21.Table 4.13 Data for Problem 2.Table 4.14 Data for Problem 4.Table 4.15 Data for Problem 5.Table 4.16 Data for Problem 6.Table 4.17 Data for Problem 7.
values for Problem 10.Table 4.5 Temperature‐pressure values for steam; Problem 11.Table 4.6 Temperature‐pressure values for gaseous ammonia; Problem 12.Table 4.7 Data for Problem 13.Table 4.8 Solutions to Exercise 4.4.9Table 4.9 Table for divided differences for quintic Hermite interpolation.Table 4.10 Divided difference table.Table 4.11 Data for Problem 13.Table 4.12 Data for Problem 21.Table 4.13 Data for Problem 2.Table 4.14 Data for Problem 4.Table 4.15 Data for Problem 5.Table 4.16 Data for Problem 6.Table 4.17 Data for Problem 7.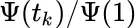 for
for 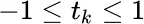 .
.










