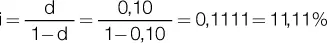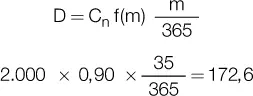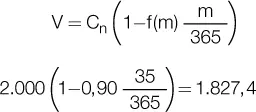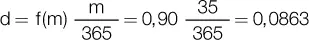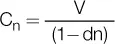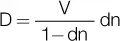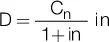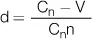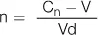Hay numerosos casos en la vida real donde aparecen operaciones que tácitamente involucran una tasa de descuento. Por ejemplo, los bienes que se venden con un precio de lista (que puede abonarse con tarjeta de crédito) o con un descuento por pago al contado. Suponga que un bien puede adquirirse según las siguientes condiciones:
Precio lista: 100 Precio al contado: 10 % de descuento
El precio de lista puede abonarse con tarjeta, y tenemos la opción de abonarlo al contado con un descuento. Supongamos que el resumen de la tarjeta habría que pagarlo dentro de 30 días. Pero la pregunta que debemos hacernos es: ¿cuál es el interés mensual que terminamos pagando si no aprovechamos el 10 % de descuento? Podemos despejar el coste de financiar la compra con tarjeta con la fórmula para despejar la tasa vencida a partir de la tasa de descuento:
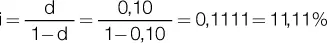
Si hubiéramos abonado la compra al contado, habríamos desembolsado 90 € (100 menos un diez por ciento). Es fácil ver que de 90 a 100 hay un 11,11 %, teniendo en cuenta que al perder el descuento, terminamos abonando 100 dentro de un mes y esto implica un coste del 11,11 %. Es posible establecer una relación de equivalencias entre tasas de descuento y tasas de interés vencidas, como se observa en la tabla 2.8:
Tabla 2.8Equivalencia entre tasas vencidas y de descuento
| d |
i |
| 10,0 % |
11,1 % |
| 20,0 % |
25,0 % |
| 30,0 % |
42,9 % |
| 40,0 % |
66,7 % |
| 50,0 % |
100,0 % |
| 60,0 % |
150,0 % |
| 70,0 % |
233,3 % |
| 80,0 % |
400,0 % |
| 90,0 % |
900,0 % |
Obsérvese cómo la diferencia entre ambas tasas aumenta a medida que aumenta el valor nominal de la tasa de descuento. Por ejemplo, para un 50 % de descuento habría que colocar el dinero al 100 % para reconstituir el capital que dio origen a la operación.
La operación de descuento en la vida real: la tasa de descuento nominal
En la práctica, el descuento de documentos se pacta generalmente con una tasa nominal anual de descuento, que llamaremos f(m), y se proporciona para la cantidad de días hasta el vencimiento del documento. De la proporción de la tasa nominal de descuento surge una tasa de descuento efectiva d para el plazo de la operación.
Ejemplo: se descuenta un documento en un banco cuando faltan 35 días para su vencimiento, pactándose una tasa nominal anual de descuento del 90 %. El descuento de la operación es:
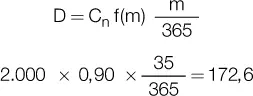
Y el valor recibido:
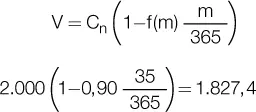
Por supuesto, la tasa nominal de descuento del 90 % implicaba una tasa efectiva de descuento para 35 días de 8,63 %:
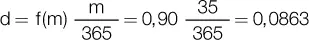
En el Capítulo 4, ahondaremos en las relaciones entre las distintas tasas, y veremos cómo es posible obtener una tasa efectiva de interés a partir de una nominal de descuento o una tasa efectiva de descuento a partir de una nominal de interés, y así sucesivamente. 4
Descuento comercial y racional: dos medidas diferentes de una misma operación
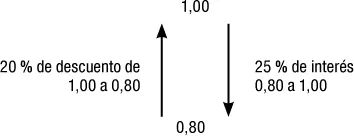
En realidad, el descuento comercial y el descuento racional son dos medidas diferentes de una misma operación. Cuando en el ejemplo anterior se descontaba una suma de 1 € por un período y se recibían 0,80 €; los 20 centavos de diferencia representaban el descuento de la operación.
Si el análisis se efectúa a partir del capital inicial de 80 € que se obtenían en préstamo, el interés abonado es del 25 % y podía considerarse que los intereses eran abonados por período vencido, como supone el descuento racional (es como si analizáramos la operación desde abajo hacia arriba).
Si la operación se analiza «desde arriba», es decir, desde el valor final de 1 € y no desde el valor presente, hay un descuento de 0,20 y representaba un interés cobrado al principio de la operación, resultando una tasa de descuento o adelantada del 20 %:
Matemáticamente, resulta fácil demostrar que el descuento racional y el comercial son lo mismo, si sustituimos en la fórmula del descuento comercial el valor de C n:
D = C ndn
Y como V = C n(1 − dn), entonces 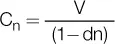
Sustituyendo C nen la expresión del descuento comercial acumulado, queda:
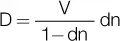
Observe que esta última expresión es igual a la expresión del descuento racional, ya que d / (1 – dn) = i, entonces quedaría D = V rin , que es igual a la expresión del descuento total para el descuento racional. También puede observarse la equivalencia si reemplazamos V ren la fórmula del descuento racional:
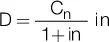
Como i / (1 + in) = d, entonces D = C ndn, que es igual a la expresión del descuento total para el descuento comercial.
Cuadro de evolución del descuento comercial
Prescindiremos ahora de la notación simbólica para mostrar una relación importante. Observe en la tabla 2.9que el valor presente del documento es igual a cero al final del quinto período:
Tabla 2.9Evolución del valor presente en el descuento comercial
| Período |
Capital al inicio |
Descuento periódico |
Valor presente |
| 1 |
1,00 |
0,20 |
0,80 |
| 2 |
0,80 |
0,20 |
0,60 |
| 3 |
0,60 |
0,20 |
0,40 |
| 4 |
0,40 |
0,20 |
0,20 |
| 5 |
0,20 |
0,20 |
0,00 |
Como en el régimen simple de descuento, este se calcula siempre sobre el valor final de la operación, el descuento periódico es constante. Las relaciones más importantes se analizan en la siguiente sección, para tratar luego el tiempo que tarda el descuento en anular el valor del documento.
Fórmulas derivadas del descuento comercial
A continuación, se muestran las fórmulas utilizadas en las operaciones de descuento comercial, haciendo la salvedad de que d es una tasa efectiva. En los casos en los que las operaciones se pactan con una tasa nominal de descuento, esta debe ser proporcionada para el período de la operación.
Tabla 2.10Fórmulas del descuento comercial
| Valor actual |
Tasa de descuento |
Número de períodos |
Descuento acumulado |
| V = C n(1 − dn) |
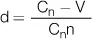 |
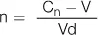 |
D(0,n) = C ndn |
Análisis del descuento comercial
Читать дальше