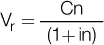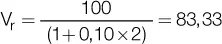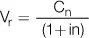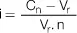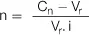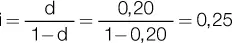El capital de 0,90 representa el valor presente de la suma de dinero futura, y la diferencia entre el capital futuro de 1 € y los 0,90 que recibimos hoy representa el descuento, que se define como la compensación, o el precio que debe pagarse por la disponibilidad inmediata de un capital antes de su vencimiento dentro de n unidades de tiempo.
El proceso de transformación de los valores futuros en valores presentes se denomina genéricamente «descuento», y a veces «actualización», y representa la contrapartida del proceso de capitalización. En el régimen simple, se distingue entre un descuento racional y un descuento comercial. Sobre la controversia acerca de si corresponde utilizar el término «descuento» o «actualización» será aclarada en una sección posterior. La diferencia entre los mismos radica en la forma en cómo se analiza la operación, siendo en el fondo, exactamente iguales. Comenzaremos describiendo el llamado descuento racional a los fines teóricos, para inmediatamente concentrarnos en las facetas del descuento comercial, por ser esta forma de calcular el descuento la más extendida en la práctica y por ser la forma en que el descuento es percibido por los agentes económicos.
Es aquel que se calcula sobre el valor presente del documento (que denominaremos V, y que es el análogo del capital inicial en el interés simple, C 0).
En el descuento racional, los intereses se calculan sobre el capital recibido, por n períodos:
D r= V rin
El valor recibido es igual al monto del documento menos el descuento:
V r= C n− D r
Y como C n= V r+ D r
Entonces C n= V r+ V rin
Si llamamos V ral valor presente con descuento racional, tenemos:
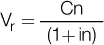
Observe que la fórmula del valor presente con descuento racional es exactamente igual a la fórmula del capital inicial en el interés simple.
Ejemplo 1: calcule el valor presente de un documento de 100 €, que vence dentro de dos meses, utilizando una tasa de interés vencida del 10 % mensual:
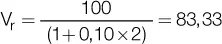
Ejemplo 2: calcule el descuento que sufrió el documento del ejemplo anterior.
D r= 83,33 × 0,10 × 2 = 16,67
Como se observa, en el descuento racional, para calcular el descuento debe calcularse previamente el valor presente del documento.
Evolución del descuento racional
Si observa la siguiente tabla verá cómo la función del descuento periódico es decreciente:
Tabla 2.6Evolución del descuento racional
| Período |
Valor presente |
Descuento periódico |
| 0 |
1 |
0 |
| 1 |
1/(1+i) |
1-1/(1+i) = i/(1+i) |
| 2 |
1/(1+i2) |
1-1/(1+i2) = i2/(1+i2) |
| 3 |
1/(1+i3) |
1-1/(1+i3) = i3/(1+i3) |
| 4 |
1/(1+i4) |
1-1/(1+i4) = i4/(1+i4) |
| . |
. |
. |
| ∞ |
0 |
1 |
Fórmulas derivadas del descuento racional
Las fórmulas son exactamente las mismas que vimos para el monto a interés simple y sus fórmulas derivadas. Recuerde que en el descuento racional los intereses se calculan sobre el capital recibido en préstamo, de ahí el nombre de «racional».
Tabla 2.7Fórmulas del descuento racional
| Valor actual |
Tasa de interés |
Número de períodos |
Descuento acumulado |
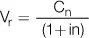 |
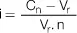 |
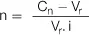 |
D(0,n) = V rin |
El descuento comercial y la tasa «anticipada» o «adelantada»
Cuando los intereses se liquidan o calculan a partir de un monto futuro, las tasas utilizadas se denominan adelantadas o de descuento. A este tipo de operatoria se la denomina «descuento comercial» o «descuento bancario», y es la más utilizada en la práctica de los negocios.
Como el descuento se practica sobre un valor final o monto (el valor final es el valor nominal del documento, sea este un pagaré, un cheque, etc.) y no sobre el capital que realmente se presta en la operación, resulta un beneficio adicional para el prestamista, como veremos a continuación.
Ejemplo: se tiene un documento de 1 € que vence dentro de 1 mes, 3 pero se decide descontarlo en una entidad financiera, para disponer de efectivo inmediatamente. El descuento es del 20 % mensual, de forma que se reciben 80 céntimos:
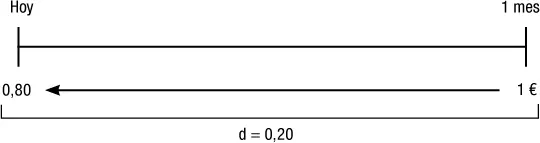
Figura 2.4Valor presente con descuento comercial.
En el descuento comercial, los intereses se calculan sobre el valor nominal del documento, que es asimilable a un capital futuro o monto (C n):
D = C ndn
De forma tal que el valor presente del documento es igual al valor nominal menos el descuento:
V = C n− C ndn
V = C n(1 − dn)
En nuestro ejemplo, el valor presente recibido es:
V = 1 − 0,20 × 1 = 0,80
Observe que el descuento se practica, a diferencia del descuento racional, sobre un valor futuro (el valor nominal del documento, que es el valor que tendrá el documento dentro de un mes), pero se recibe en préstamo una suma menor (0,80). Por lo tanto, el prestamista gana un rendimiento que es igual al descuento (d) sobre la cantidad que efectivamente presta (1-d):

¿Cuál es el rendimiento que obtuvo el prestamista si cobró el 20 % de interés sobre un capital de 1 € y en realidad solo prestó 0,80? Obviamente, es mayor que el 20 %, pues si colocáramos el dinero obtenido en préstamo al 20 % apenas alcanzaríamos 96 céntimos:
0,80 × (1 + 0,20) = 0,96
La tasa de interés implícita o equivalente en la operación anterior puede despejarse fácilmente razonando cuál es la tasa de interés vencida a la que tendríamos que colocar el capital obtenido en préstamo (1 – d), para reconstruir el euro que dio origen a la operación:
(1 − d)(1 + i) = 1
0,80(1 + i) = 1
Donde la tasa de interés vencida i resulta ser del 25 %, resultado al que también llegamos razonando el rendimiento que tuvo el prestamista:
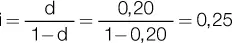
Este tipo de descuento tiene una característica distintiva: la tasa que se utiliza en la operación es una tasa de descuento o adelantada, ya que se calcula sobre el valor que el documento tendrá en el futuro. A esta tasa de descuento le corresponda una tasa equivalente i vencida, que en nuestro ejemplo resulta ser del 25 %. Por lo tanto, el verdadero coste efectivo de la operación de descuento siempre hay que medirlo en términos de tasa de interés vencida.
Читать дальше