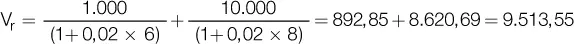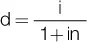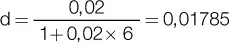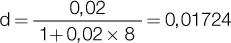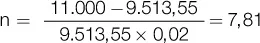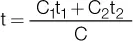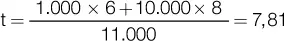Guillermo L. Dumrauf - Manual de matemáticas financieras

a. Por descuento racional

El primer paso es calcular el valor presente de los dos documentos, para obtener el valor presente del nuevo documento, que se firmará con un vencimiento a diez meses:

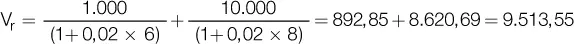
Luego se calcula el valor nominal del nuevo documento mediante la fórmula del monto a interés simple, para diez períodos:

C 10= 9.513,55 (1 + 0,02 × 10) = 11.416,25

El nuevo documento, firmado con vencimiento dentro de diez meses por un valor de 11.416,25 €, es equivalente a los dos documentos por 1.000 y 10.000 euros, que vencían dentro de 6 y 8 meses, respectivamente.

Un punto muy importante que debe remarcarse es que en el régimen simple siempre debe calcularse primero el valor presente del documento, para después calcular su equivalente en otra fecha futura. Por ejemplo, el documento de 1.000 € que vencía a los 6 meses tiene un valor presente de 892,85; la diferencia de 107,15 son los intereses entre el momento 0 y el mes 6; si capitalizáramos el valor nominal del documento (1.000) para llevarlo directamente a la fecha futura donde vencerá el nuevo documento, esto sería incorrecto, puesto que se estaría capitalizando los intereses y se transformaría la operación en una de interés compuesto.

b. Por descuento comercial

Si la tasa de interés vencida es del 2 % mensual, la tasa de descuento equivalente es influida por el número de períodos, según vimos antes en este mismo capítulo, donde la obteníamos a partir de la siguiente expresión:

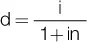
Para el primer documento, la d equivalente para 6 meses es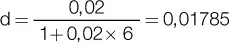

Y para el segundo documento la d equivalente para 8 meses es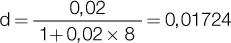

Luego, resolvemos el valor presente de ambos documentos:

V = V 1+ V 2

V = 1.000 (1 – 0,01785 × 6) + 10.000 (1 – 0,01724 × 8) = 9.513,55

Que es el mismo valor obtenido a través de la fórmula del valor presente con descuento racional que vimos anteriormente. El valor nominal del nuevo documento también se calcula igual que antes, mediante la fórmula del monto a interés simple, para diez períodos:

C 10= 9.513,55 (1 + 0,02 × 10) = 11.416,25

Se habla de vencimiento medio cuando solo se modifica el plazo de vencimiento (es decir, que no se le cambia el valor a los pagos, ya que en este caso los capitales se reemplazan por un capital C tque es igual a la suma de los capitales originales. Siguiendo con el ejemplo anterior, donde el valor presente de los dos documentos por reemplazar era de 9.513,55 €, debemos resolver el momento en que ese valor iguala a la suma de los dos documentos (C 1+ C 2).

Para obtener el plazo de vencimiento, se recurre a la fórmula que obtiene el número de períodos y que habíamos deducido de la fórmula del monto a interés simple:

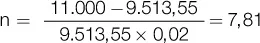
La parte fraccionaria de la respuesta (0,81 meses), debe interpretarse como el 81 % de un mes de 30 días, lo que significaría que el plazo sería igual a 7 meses y 24 días.

A diferencia del vencimiento común, cuando tenemos un problema de vencimiento medio la incógnita puede ser una sola: el número de períodos, ya que el valor nominal del nuevo documento es predefinido como la suma de los valores nominales de los documentos que reemplaza y, por lo tanto, no es una incógnita.

Observe que el valor del número de períodos se ubica entre los dos vencimientos, como no podía ser de otra manera. Si lo analizamos desde los límites, el vencimiento común nunca podría haber caído en el período 6 o en el 8. En el primer caso, porque el valor presente de 10.000 € haría que la suma de los dos documentos sea menor que 11.000 €; y en el segundo porque en el período ocho 1.000 € capitalizados haría que la suma sea mayor que 11.000 €. Por lo tanto, necesariamente el vencimiento común debe ubicarse en el medio de los vencimientos. ¿Más cerca de 6 o de 8? La fecha del vencimiento común dependerá de dos cosas: a) el valor nominal de los documentos y b) la tasa de interés. El lector puede comprobar por su cuenta que:

• Si el orden de los vencimientos se hubiera invertido, con 10.000 venciendo en el mes 6 y 1.000 venciendo en el mes 8, el vencimiento común sería 6,17.

• Si la tasa de interés hubiera sido del veinte en lugar del dos por ciento, el vencimiento común caería en 7,79.

a. En el descuento racional

El último punto de la sección anterior ilustraba una relación muy importante: aun para grandes cambios en la tasa de interés vencida, el vencimiento medio —en el descuento racional— se modifica muy poco. ¿A qué se debe? Cuando la tasa de interés aumenta, hay dos fuerzas que juegan en sentido contrario: por un lado crece el monto del documento cuya fecha de vencimiento es anterior a la del vencimiento medio y, por otro, se reduce el valor presente del documento cuyo vencimiento es posterior a la fecha del vencimiento medio.

En general, el vencimiento medio se mueve hacia la fecha de vencimiento del documento de mayor valor, pero un aumento en la tasa de interés produce el siguiente cambio: si el vencimiento del documento con mayor valor es el más lejano, el vencimiento medio se reduce; si por el contrario, el vencimiento es anterior al del documento con menor valor, el aumento de la tasa lo acerca a su fecha de vencimiento. Lo contrario se cumple para reducciones en la tasa de interés. Estos efectos son todavía más importantes en el régimen compuesto, y conocer esta relación tiene particular importancia en situaciones de la vida real, por ejemplo, en el diseño de carteras «inmunizadas» de títulos de renta fija.

b. En el descuento comercial

El caso del vencimiento medio en el descuento comercial plantea un caso interesante, ya que puede calcularse independientemente de la tasa de contrato de la operación. El principio de equivalencia nos dice que el valor presente del nuevo documento es igual a la suma de los valores presentes de los documentos que reemplaza:

C (1 − dt) = C 1(1 − dt 1) + C 2(1 − dt 2)

Distribuyendo y luego sacando el factor común queda:

C − Cdt = C 1− C 1dt 1+ C 2− C 2dt 2

Como en el vencimiento medio, en el nuevo documento C = C 1+ C 2podemos simplificar la ecuación y queda:

Cdt = d (C 1t 1+ C 2t 2)

Finalmente, podemos despejar t:

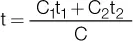
Para el ejemplo anterior, resulta:

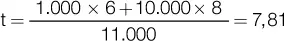
Y si se invirtieran los vencimientos, como fue mencionado anteriormente, el período t hubiera sido de nuevo 6,17: