Guillermo L. Dumrauf - Manual de matemáticas financieras

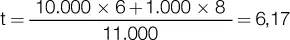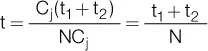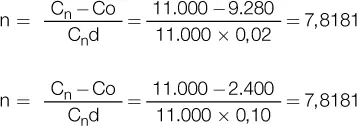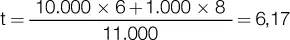
En el caso particular de que C 1= C 2la fórmula quedaría:

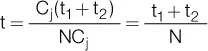
Donde N representa el número de documentos. Observe que en estas expresiones no aparece la tasa de descuento de la operación. El resultado hubiera sido el mismo aunque la tasa de descuento hubiera sido del 2 % o del 200 %. Sin embargo, vimos que cuando aplicábamos el descuento racional, un cambio en la tasa de interés vencida tenía influencia, aunque muy poca, en el vencimiento medio de la operación. ¿Por qué en el descuento comercial el cambio en la tasa de descuento no influye sobre el resultado? Ya vimos que para que el descuento comercial y el racional arrojen exactamente el mismo resultado, tendríamos que utilizar para cada documento la tasa equivalente para cada período, según el vencimiento de cada documento. Así, tendríamos que calcular la d equivalente a la i en cada período, ya que la relación se ve alterada por el número de períodos, como fue demostrado anteriormente. En cambio, si utilizamos el descuento comercial y se predefine una tasa de contrato d, si bien es cierto que, cuanto mayor sea esta, menor será el valor presente de los documentos, inmediatamente aparece implícita una tasa vencida de arbitraje que iguala el valor presente con la suma de los documentos (11.000) siempre en idéntico plazo. Por ejemplo, si hacemos el cálculo con tasas de descuento de d = 2 % y d = 10 % mensual, el valor presente de los documentos en cada caso sería:

V (d=2%)= 1.000 (1 – 0,02 × 6) + 10.000 (1 – 0,02 × 8) = 9.280

V (d=10%)= 1.000 (1 – 0,10 × 6) + 10.000 (1 – 0,10 × 8) = 2.400

Luego el vencimiento medio en ambos casos sería:

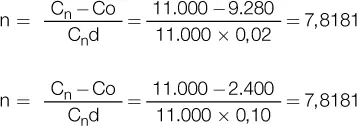
Siempre hay implícita una tasa de interés vencida que hace que la colocación de 9.280 o de 2.400 (2,37 % mensual y 45,83 % mensual) alcance en 7,8181 períodos el monto de 11.000 €:

9.280 (1 + 0,0237 × 7,8181) = 11.000

2.400 (1 + 0,4583 × 7,8181) = 11.000

Por lo tanto, la tasa de descuento no influye en el vencimiento medio, ya que si esta aumenta, y con ello disminuye el valor presente de los documentos, luego surge una tasa de interés vencida mayor que vuelve a igualar el valor presente con la suma de los documentos siempre en el mismo plazo. 7

Preguntas de autoevaluación

1. ¿Por qué en el cálculo del vencimiento común o el vencimiento medio debemos siempre calcular primero el valor presente?

2. ¿Por qué la tasa no influye en el vencimiento medio en el descuento comercial?

Entendemos por régimen de interés simple aquel donde los intereses se calculan sobre el capital inicial. En la vida real, tenemos ejemplos de cálculo de los intereses bajo el régimen simple como los depósitos a plazo fijo, los intereses de la caja de ahorros en el interior del período de capitalización, los ajustes de deudas impositivas, indemnizaciones y otros.

En las operaciones de descuento, este se practica siempre sobre el valor nominal del documento, dando lugar a la conocida tasa «adelantada», «anticipada» o de descuento comercial, que involucra una tasa de interés vencida «implícita». Esta última es la que debe considerarse a la hora de establecer el verdadero coste financiero de una operación de descuento.

Por último, el principio de equivalencia de capitales nos dice que dos capitales son equivalentes cuando tienen el mismo valor presente. Esto es relevante en el caso de reemplazo de pagos para el vencimiento común y el vencimiento medio.

1. Marque la respuesta correcta en la siguiente afirmación: «En el régimen simple, si las tasas de interés cambian período a período, para calcular el monto dentro de n períodos, estas deben»:

a. Sumarse en la expresión (1 + i 1+ i 2+ … i n)

b. Multiplicarse en los siguientes factores (1 + i 1) (1 + i 2) … (1 + i n)

2. Marque cuáles de los siguientes atributos tiene una tasa nominal:

a. Representa la tasa contractual de la operación.

b. Es una tasa vencida, a interés simple.

c. Si contratamos un plazo fijo al 6 % anual por 30 días, y lo renovamos cada 30 días, el rendimiento efectivo anual siempre será igual a la tasa nominal anual del 6 %.

d. Es un coeficiente de comparación, sirve para comparar entre tasas nominales.

e. Si el período de capitalización es igual a 1 (uno), coincide con la tasa efectiva de la operación.

6. Marque la respuesta correspondiente en las siguientes expresiones:

a. En el régimen simple de intereses, el interés periódico es: (constante / creciente / decreciente). En consecuencia, las tasas efectivas periódicas son (constantes / crecientes / decrecientes).

b. En el descuento comercial, el descuento periódico es: (constante / creciente / decreciente). En consecuencia, las tasas efectivas periódicas de descuento son (constantes / crecientes / decrecientes).

c. El valor (máximo / mínimo) que puede tomar la tasa utilizada en una operación realizada por el descuento comercial en un régimen simple (varia proporcionalmente con la tasa de interés utilizada en la operación / depende del valor que adquiere el importe por descontar / es igual al inverso del número de períodos que tiene la operación).

4. Para poder utilizar la fórmula del monto a interés simple C n= C 0(1 + in), la condición es:

a. Que la tasa de interés se mantenga período a período.

b. Que la tasa de interés se mantenga período a período y además los períodos tengan la misma duración.

5. En el régimen simple de interés, la expresión d / (1 – d) = i permite obtener la tasa de interés vencida equivalente a la aplicada en una operación de descuento comercial. Señale cuál es la tasa de descuento efectiva de la operación cuando n ≠ 1, si en ese caso d es una tasa nominal o efectiva y a qué se debe. Por último, explique en la relación inversa d = i / (1 + i.n), con respecto a i, cuál es la tasa efectiva y la nominal. Además, mencione en qué caso tanto d como i pueden ser tasas nominales y efectivas de una operación al mismo tiempo.

6. Un individuo retira todos los meses el interés que le produce una cuenta de ahorros y utiliza ese dinero para vivir. Por la forma en que se realiza la operación, se asemeja al régimen simple. ¿Por qué? ¿Qué tendría que ocurrir para que dicha operación se transforme en régimen compuesto?

7. El descuento racional y el comercial son dos medidas diferentes de una misma operación. ¿En qué se diferencian?

8. ¿Por qué en el vencimiento medio siempre el plazo de vencimiento cae entre los documentos que se reemplazan? ¿Por qué nunca puede caer en un extremo? ¿Cuáles son las dos variables que lo acercan más al vencimiento de alguno de los documentos que se reemplazan?

9. Responda cuál de las siguientes equivalencias son correctas:

a. Un aumento de 14 veces = 1.300 % más

b. Una disminución de 2 veces = -100 %

c. Un aumento de 10 veces = 1.000 %

10. Si el peso colombiano cotiza a 1.810 $ por dólar el 18/2/2013 y el 19/2/2013 cotiza a 1.830 $ por dólar, tuvo un aumento diario de:

a. 1 %

b. 1,10 %

La mayoría de los problemas, cuando existe una tasa nominal como dato, han sido resueltos suponiendo un año civil de 365 días, con excepción de los problemas 11, 15 y 16. No obstante, la utilización de un año comercial o civil es una cuestión de la legislación que rige para cada contrato financiero según cada país. Utilizar un año de 360 o 365 días para las resoluciones conduce a respuestas ligeramente diferentes.