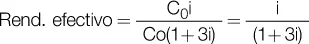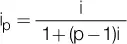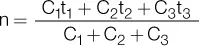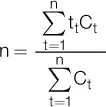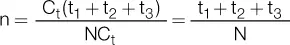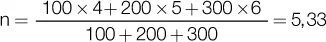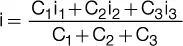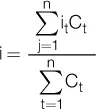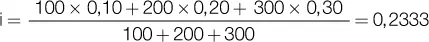Tabla 2.5Interés periódico y rendimiento efectivo en el régimen simple
| T |
Capital |
Interes periódico |
Monto |
Rendimiento efectivo |
| 1 |
100 |
10 |
110 |
10 % |
| 2 |
110 |
10 |
120 |
9,09 % |
| 3 |
120 |
10 |
130 |
8,33 % |
| 4 |
130 |
10 |
140 |
7,69 % |
El rendimiento efectivo es calculado dividiendo el interés periódico por el capital al inicio. Así, para el primer período es el 10 %, (10 / 100) – 1, pero para el segundo se reduce al 9,09 %, pues el interés periódico sigue siendo de 10 €, pero representa un porcentaje menor de un capital de 110 €. Es claro que mientras el interés periódico se mantenga constante, representará un porcentaje menor comparado con el capital inicial. Por lo tanto, el rendimiento efectivo en el régimen simple es decreciente. Por ejemplo, para calcular el rendimiento efectivo del período 4, tendríamos que comparar el interés periódico (que es siempre constante) contra el capital al final del período 3:
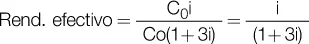
Generalizando, para obtener el rendimiento de un período cualquiera hacemos:
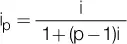
De la expresión anterior se deduce que si el numerador es constante y el denominador es creciente (ya que cuando aumenta el número de períodos p también aumenta), el rendimiento periódico es decreciente.
Suponiendo que tres capitales C 1, C 2y C 3son colocados durante diferentes plazos t 1, t 2y t 3, se denomina plazo medio n al tiempo durante el cual debe ser colocada la suma de esos capitales, a la misma tasa, de modo que el interés producido sea igual a la suma de los intereses producidos por cada uno de los capitales C 1, C 2y C 3:
(C 1+ C 2+ C 3) in = C 1it 1+ C 2it 2+ C 3it 3
Dividiendo ambos miembros por i y despejando el valor de n, obtendremos:
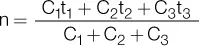
Esta última fórmula nos permite obtener las siguientes conclusiones:
a. El plazo medio es independiente de la tasa de interés común.
b. El plazo medio es la media aritmética ponderada de los plazos.
La conclusión b nos permite establecer una fórmula general para el plazo medio, que es igual a la sumatoria de los plazos ponderados:
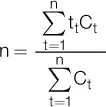
La fórmula del plazo medio puede ser establecida para cualquier unidad común de plazos, y el valor de la incógnita n se referirá a una unidad de tiempo común de los plazos t 1, t 2y t 3. En particular, si C 1= C 2= C 3,podemos sacar el factor común en la expresión anterior y nos queda:
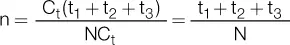
Donde N representa la cantidad de capitales (N = 3 en este caso) y observamos que, en este caso, el plazo medio será el promedio simple de los plazos dados.
Ejemplo: tres capitales de 100, 200 y 300 fueron colocados a la misma tasa del 10 % mensual durante 4, 5 y 6 meses, respectivamente. Calculamos ahora durante cuánto tiempo tendría que estar aplicada la suma de esos capitales, a la misma tasa, para que los intereses sean iguales a la suma de los intereses de esos capitales en los plazos dados.
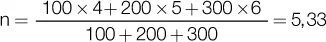
Suponiendo que tres capitales C 1, C 2y C 3sean colocados durante n períodos a tasas diferentes i 1, i 2y i 3, se denomina tasa media de una operación a la que debe ser colocada la suma de esos capitales durante n períodos, para que produzcan un interés que iguale la suma de los intereses que produce cada uno de los capitales C 1, C 2y C 3:
(C 1+ C 2+ C 3)in = C 1i 1n + C 2i 2n + C 3i 3n
Podemos sacar el factor común n en el segundo término y luego despejamos la tasa media:
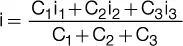
De la fórmula se observa que:
a. La tasa media es independiente del plazo común al que fueron colocados los depósitos.
b. La tasa media es la media aritmética ponderada de tasas.
La conclusión b nos permite establecer una fórmula general para la tasa media, que es igual a la sumatoria de las tasas ponderadas:
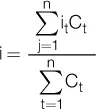
En particular, si C 1= C 2= C 3, se puede sacar el factor común C jy la fórmula de i se simplifica por la siguiente:

En este último caso particular, la tasa media es el promedio simple de las tasas dadas. N representa la cantidad de capitales (N = 3 en este caso).
Ejemplo: tres capitales de 100, 200 y 300 fueron colocados con tasas de interés mensuales del 10 %, 20 % y 30 %, respectivamente, durante un mes. Calculamos ahora cuál fue la tasa media de la operación:
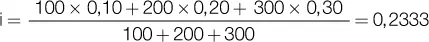
Preguntas de autoevaluación
1. ¿La fórmula genérica del monto a interés simple puede usarse en cualquier caso?
2. ¿Por qué las tasas se suman en el régimen simple en lugar de multiplicarse?
3. ¿Cuál es la diferencia entre el interés exacto y el interés comercial?
4. ¿Por qué en el régimen simple las tasas son proporcionales y al mismo tiempo equivalentes?
2.3 Descuento simple
Descuento racional y tasa de interés vencida
Cuando definimos el monto de un capital, se estableció una relación directa entre el capital inicial y el valor final del mismo, sujeto a un régimen de capitalización a una tasa de interés i por un número de unidades de tiempo que llamamos n.
Supondremos inicialmente una operación genérica de descuento: queremos disponer hoy de una suma de dinero que tenemos que cobrar dentro de 1 año por 1 €; por su disponibilidad inmediata, nos descontarán los intereses que representan la diferencia entre el capital disponible dentro de un año y su valor presente.

Figura 2.3Valor presente con descuento racional.
Читать дальше