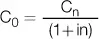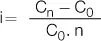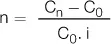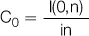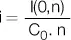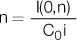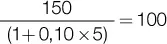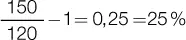1 ...7 8 9 11 12 13 ...22 El régimen simple existe tanto en sentido positivo del tiempo (capitalización) como en sentido negativo del mismo (descuento). En la capitalización vamos desde el presente hacia el futuro cuando depositamos una suma de dinero que gana interés durante un cierto período de tiempo, y en el descuento recorremos el camino inverso cuando calculamos el valor presente de un capital futuro. También veremos que es posible hablar de una tasa de interés vencida y una tasa de descuento o anticipada.
En la vida real, existen numerosas situaciones donde nos encontraremos con el interés simple. ¿Quién no ha realizado alguna vez un depósito a plazo en una institución bancaria? En este caso, los depósitos ganan un interés que se calcula sobre el capital inicial de la operación, por un período de tiempo determinado que puede ser un mes, dos meses, etc. Puesto que no hay capitalización de intereses en el período por el que se realiza el plazo fijo, estos son calculados de acuerdo a las reglas del interés simple. También los intereses de la caja de ahorros dentro del período de capitalización, los préstamos que calculan intereses directos sobre el capital, algunos ajustes de deudas impositivas y algunos casos de sentencias judiciales son ejemplos donde se aplica el interés simple.
En este capítulo veremos las principales operaciones que se realizan mediante el régimen simple, incluyendo el descuento comercial, una operación muy extendida en la práctica. Estableceremos la equivalencia fundamental entre la tasa de interés vencida y la tasa de descuento, y finalmente realizaremos una introducción a la equivalencia de capitales que se encuentran expresados en diferentes momentos de tiempo.
Después de leer este capítulo, usted debería ser capaz de:
• Calcular el monto de un depósito a plazo fijo y el interés de la operación.
• Calcular el valor presente en una operación de descuento.
• Calcular una tasa proporcional.
• Calcular un capital equivalente dando un vencimiento común a documentos que vencen en diferentes fechas.
2.2 Monto a interés simple
Las características principales del monto a interés simple son las siguientes:
1. Los intereses se calculan siempre sobre el capital inicial, de forma que los intereses no generan nuevos intereses, el capital inicial permanece constante hasta la fecha en que haya sido convenido su reembolso. 1
2. Se deduce de 1 que los intereses representan una suma fija, no existe, por lo tanto, capitalización de intereses.
3. Los intereses son proporcionales al capital, al tiempo y a la tasa de interés de la operación.
La mejor forma de apreciar las variables que componen una operación de interés simple y su evolución es observar el cuadro que se desarrolla a continuación:
Evolución del interés simple
Supongamos un capital inicial C 0= 1 € que se coloca a interés simple y veamos cómo se transforma a lo largo de n períodos para obtener la fórmula «genérica» del monto a interés simple:
Tabla 2.1Evolución del interés simple
| Período |
Capital inicial |
Interés periódico |
Monto |
| 1 |
C 0 |
I(0,1) = C 0i |
C 1= C 0+C 0i = C 0(1+i) |
| 2 |
C 0(1+i) |
I(1,2) = C 0i |
C 2= C 0(1+i) + C 0i = C 0(1+2i) |
| 3 |
C 0(1+2i) |
I(2,3) = C 0i |
C 3= C 0(1+2i) + C 0i = C 0(1+3i) |
| n |
C 0[1+(n–1)i] |
I(n–1,n) = C 0i |
C n= C 0[1+(n–1)i] + C 0i = C 0(1+ni) |
En general, para un período cualquiera que llamaremos p, el interés periódico será I (p – 1,p) = i, y el capital final:
C p= C 0(1 + pi)
Que se lee como el capital original multiplicado por 1 + «p veces» la tasa de interés. Por lo tanto, el capital final o monto del último período será C n= C 0(1 + ni).
Note que para obtener esta expresión solo multiplicamos el capital original de la operación por el factor de capitalización (1 + ni) transformando el capital inicial en un capital equivalente final o monto. Por ejemplo, si contáramos con 100 € que se invierten durante 5 meses a una tasa de interés del 2 % mensual, al final del plazo tendremos:
100 (1 + 0,02 × 5) = 110
En la actividad financiera cotidiana, la tasa de interés se expresa en tanto por ciento. Así, 2 % equivale a 2 / 100 = 0,02. Para los cálculos, siempre expresamos la tasa en tanto por uno.
Fórmulas derivadas del monto a interés simple
Las fórmulas que se derivan de la fórmula genérica del monto a interés simple solo requieren simples despejes de términos. Realizaremos algunos comentarios respecto a ellas por que creemos que pueden revestir interés.
Tabla 2.2Fórmulas del interés simple
| Capital inicial |
Tasa de interés |
Número de períodos |
Interés acumulado |
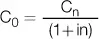 |
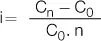 |
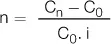 |
I(0,n) = C 0in |
| o también |
o también |
o también |
o también |
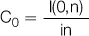 |
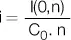 |
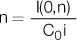 |
I(0,n) = C n− C 0 |
a. Fórmula del capital inicial
Simplemente, el capital inicial se obtiene descontando por n períodos el monto o capital final. Por caso, un capital final de 150 €, que fue obtenido con una tasa de interés del 10 % al cabo de 5 períodos, tiene hoy un valor de:
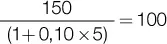
b. Fórmula de la tasa de interés
Esta fórmula es muy intuitiva, ya que se aplica muchas veces de manera automática para obtener porcentajes de rendimiento, aunque no se concozca su naturaleza. Piense por un momento que usted vende un bien a 150 € que adquirió cierto tiempo atrás por 120 €. El tiempo que media representa el período de la operación que para nosotros será igual a 1 (1 mes, 1 bimestre, un período de cierta cantidad de días, no importa realmente cuánto tiempo, para nosotros representa un período en este caso). Ahora supongamos que usted quiere conocer el porcentaje de rendimiento de esa operación. El cálculo intuitivo es tomar los 150, dividirlo por 120 y restar el 1 (uno):
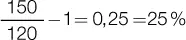
Pues bien, la tasa de interés se calcula de esa forma, ya que representa la fórmula que resulta de obtener la tasa a partir de la fórmula del monto:
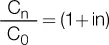
Si n = 1 y pasamos restando el 1, tenemos la fórmula que tantas veces se utiliza para calcular rápidamente un porcentaje de rendimiento:
Читать дальше