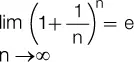Son aquellas en las cuales cada uno de los términos se obtiene multiplicando al anterior por un número constante q llamado razón. La progresión 3, 6, 12, 24, 48, 96 es geométrica de razón q = 2, pues cada término es igual al anterior multiplicado por 2. Por ejemplo, los intereses que se acumulan en el régimen de interés compuesto, constituyen una progresión geométrica creciente. También el valor presente de las cuotas de un préstamo constituye una progresión geométrica, que en este caso es decreciente.
El cálculo de un término cualquiera a nse puede obtener directamente haciendo:
a n= a 1q n−1
En el ejemplo 0, el 5.º término es:
a 5= 3.2 4= 3 × 16 = 48
Suma de todos los términos: en una progresión geométrica finita, la suma de los términos de esta se calcula con las siguientes fórmulas:
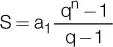 para progresiones crecientes.
para progresiones crecientes.
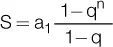 para progresiones decrecientes.
para progresiones decrecientes.
Si la progresión geométrica tiene infinitos términos, con una razón 0 < q < 1, la última fórmula expresada se transforma del siguiente modo:
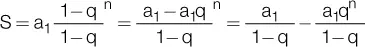
Observe que en el 2.º término del resultado, si n→∞ entonces q n→0 por ser 0 < q < 1, con lo cual, se anula todo ese término y queda:
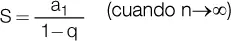
A la función f(x) = b x, donde b > 0, b ≠ 1 y el exponente x es cualquier número real, se la denomina función exponencial con base b. En la figura 1.5, se muestran las gráficas de dos funciones exponenciales, donde se puede observar que existen dos formas básicas, dependiendo de si la base b > 1 o bien b < 1. Si b > 1, entonces la gráfica de y = 2 xasciende de izquierda a derecha; es decir, al aumentar x también se incrementa y, mientras que la función y = (1/2) desciende de izquierda a derecha, es decir, que al aumentar x disminuye el valor de y. A la función ascendente, se la puede asimilar al monto a interés compuesto (1+i) ny a la función descendente se la puede asimilar a la función 1/(1+i) n.
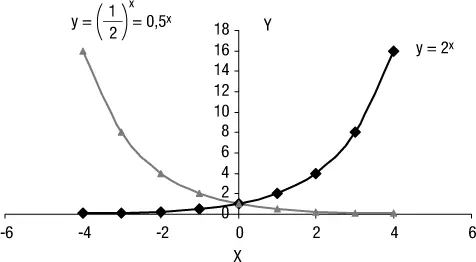
Figura 1.5Función exponencial.
La función exponencial natural
Uno de los números más útiles como base para las funciones exponenciales es el número irracional denotado por la letra e en honor al matemático suizo Leonard Euler. Sus primeras cifras son 2,718281. Aunque este número parece raro para ser la base de una función exponencial, es muy utilizado en finanzas y en economía, principalmente para modelizar funciones de crecimiento y disminución de precios cuando se asume que se producen en forma continua.
El número e se obtiene al resolver un binomio del tipo 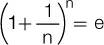 cuando n tiende a infinito, y puede comprobarse que cuando aumenta n, el valor de e se estabiliza en 2,718281:
cuando n tiende a infinito, y puede comprobarse que cuando aumenta n, el valor de e se estabiliza en 2,718281:
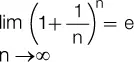
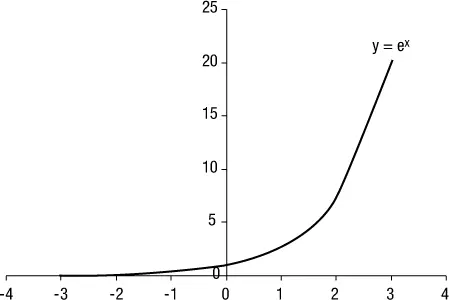
Figura 1.6Función exponencial natural.
Para comprender mejor la utilización del número e en finanzas, pensemos en un ejemplo. Si un activo financiero tiene hoy un precio de 100 € y este crece al 5 % anual en forma continua (el 5 % se compone continuamente) dentro de un año su valor será:
100e 0,05= 105,127
La función logarítmica es la inversa de la función exponencial, ya que la función logarítmica invierte la acción de la función y viceversa. Si se calculó el valor de una función exponencial, por ejemplo, un monto a interés compuesto, para un dato de entrada x (tiempo) se obtuvo un resultado y (monto); en cambio, en la función logarítmica, el dato de entrada es el monto y se obtiene el exponente. Entonces, el logaritmo de un número es un exponente. Concretamente, es el de la potencia a la que se debe elevar la base (que cuando es el número e, se denomina logaritmo natural) para obtener el monto. Por ejemplo:
Log 2,71828 = 2,079 porque 2,7182 2,079= 8
Entonces, para calcular el logaritmo de x en base b, se expresa y = Log bx, y significa que b y= x. De manera que el resultado y es la potencia a la que se debe elevar la base para obtener como resultado x.
La función logarítmica invierte la función exponencial. En las figuras 1.7y 1.8, se muestran las gráficas de la función exponencial del monto y = f(x) y su inversa logarítmica. Observe que en la función monto, para un tiempo dado, surge un monto, mientras que en la función logarítmica, para ese monto, hay como resultado el exponente correspondiente.
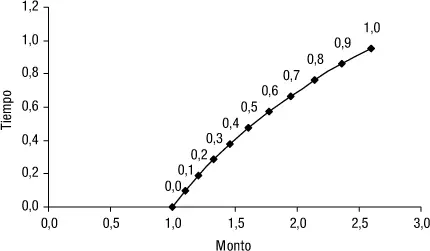
Figura 1.7Función exponencial.
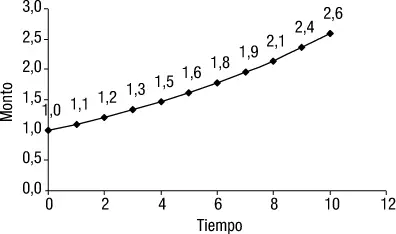
Figura 1.8Función logarítmica.
Dados dos números reales y positivos n y b, se llama logaritmo del número n en base b al número x, siendo x el número al cual hay que elevar b para obtener n:
log bn = x si y solo si b x= n
Por ejemplo, log 24 = 2 si y solo si 2 2= 4.
Hasta aquí estaríamos hablando de un logaritmo común, pero si consideramos que la base b es igual al número e —que describimos en la Sección 2.4—, entonces estaríamos en presencia de un logaritmo natural, o también denominado neperiano. Por ejemplo:
Ln 10 = 2,302585 y e 2,302585= 10
La función y = ln(x) se define solo para x > 0 y aparece en la figura 1.9. Para obtenerla, se puede insertar cualquier valor x > 0 y obtener ln(x) usando una calculadora o una hoja de cálculo. Recuerde que no existe el logaritmo de un número negativo, en cambio, el logaritmo de cualquier número menor que 1 (uno) da un número negativo.
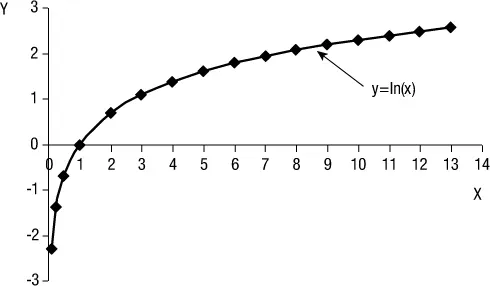
Figura 1.9Función logaritmo natural.
Se puede observar en la figura 1.9que:
• Ln(x) < 0 para 0 < x < 1.
• Ln(1) = 0 (que corresponde a la intersección con el eje x (1,0). Esto se entiende ya que habría que elevar a 0 (cero) la base para obtener 1 (uno).
• Ln(x) > 0 para x > 1.
Читать дальше

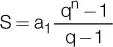 para progresiones crecientes.
para progresiones crecientes.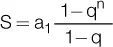 para progresiones decrecientes.
para progresiones decrecientes.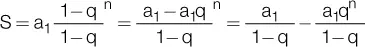
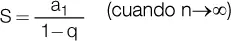

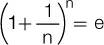 cuando n tiende a infinito, y puede comprobarse que cuando aumenta n, el valor de e se estabiliza en 2,718281:
cuando n tiende a infinito, y puede comprobarse que cuando aumenta n, el valor de e se estabiliza en 2,718281: