Guillermo L. Dumrauf - Manual de matemáticas financieras
Здесь есть возможность читать онлайн «Guillermo L. Dumrauf - Manual de matemáticas financieras» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на испанском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Manual de matemáticas financieras
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:4 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Manual de matemáticas financieras: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Manual de matemáticas financieras»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
Este libro ha sido preparado de tal manera que pueda alcanzar el entrenamiento necesario para desenvolverse y progresar con ductilidad en el estudio de la materia, respetando los siguientes ejes:
• Tratamiento ameno pero riguroso de la teoría
• Ejercitación práctica con resoluciones comentadas
• Aplicación a problemas del mundo real
Asimismo, el libro cuenta con recursos adicionales que se pueden descargar gratis desde www.marcombo.info para reforzar los conocimientos aprendidos sobre la materia, como comentarios a las resoluciones de los ejercicios, que serán muy útiles para facilitar la comprensión de los temas.
Si es un estudiante de las carreras de grado y posgrado de económicas, finanzas o ingenierías, un ejecutivo financiero u otro profesional que utiliza las matemáticas financieras en su labor cotidiana, este libro será su gran aliado.
Guillermo L. Dumrauf: Doctor en Ciencias Económicas por la Universidad de Buenos Aires y consultor económico financiero, es profesor titular en prestigiosas universidades y autor de 12 libros de finanzas, matemáticas aplicadas a las finanzas y macroeconomía. Asimismo, ha escrito numerosas publicaciones, colabora en revistas y participa en infinidad de congresos. Es conferencista internacional y miembro de comités académicos en maestrías y doctorados.

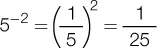
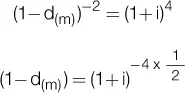
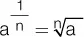

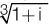 .
.