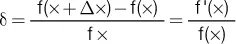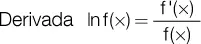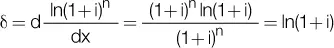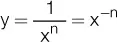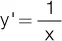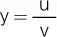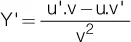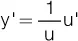1 ...6 7 8 10 11 12 ...22 Los números negativos y el 0 no tienen logaritmos. El ámbito son todos los números reales. Los números entre 0 y 1 tienen logaritmos negativos, y conforme más cercano está el valor de x a cero, más negativo es su logaritmo. No existe ordenada en el origen.
Propiedades de los logaritmos
1. Logaritmo de un producto: es igual a la suma de los logaritmos de los factores.
log (a · b · c) = log a + log b + log c
2. Logaritmo de un cociente: es igual al logaritmo del dividendo menos el logaritmo del divisor.
log (m : n) = log m − log n
3. Logaritmo de una potencia: es igual al exponente multiplicado por el logaritmo de la base.
log a n= n · log a
4. Logaritmo de una raíz: es igual al logaritmo del radicando dividido por el índice de la raíz.
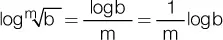
En matemáticas financieras, es común utilizar logaritmos para despejar un exponente como es el tiempo n, por ejemplo, en las fórmulas del interés compuesto. Sea, por ejemplo, la función del monto a interés compuesto Co (1+i) n= Cn. Si despejamos n queda:
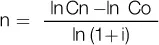
La derivada de una función f se denota por f’ (se lee «f prima») y está definida por 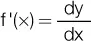 .
.
Esta relación podemos representarla en un gráfico de la función monto a interés compuesto donde f’(x) es el interés de un infinitésimo de tiempo, cuando Dx representa una intervalo de tiempo muy pequeño, que tiende a cero.
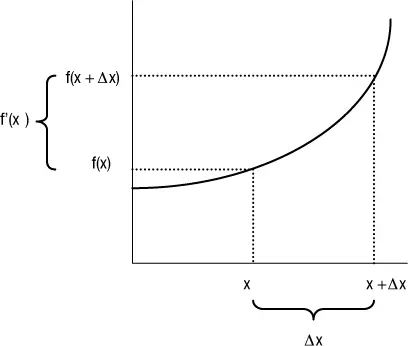
Figura 1.10Función f(x).
Entonces lo que interesa ver es el cambio que se produce en el valor de la función para un pequeñísimo cambio en x. Si se puede evaluar f’(x), se dice que f es diferenciable y a f’(x) se le denomina «derivada de f en x» o la «derivada de f con respecto a x». Tenga presente que dy/dx no se considera como un cociente sino como un diferencial; al proceso de determinar la derivada se le denomina diferenciación. Además de f’(x) otras notaciones para la derivada de y = f(x) en x, son dy/dx (que se lee “de y en de x” y también y’ (se lee “y prima”).
Cálculo de la tasa de interés instantánea
Si ahora realizamos el cociente entre el interés ganado en un infinitésimo de tiempo y el capital invertido, obtenemos la tasa de interés de un infinitésimo de tiempo, que como sabemos recibe el nombre de tasa instantánea:
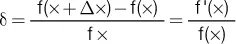
De manera que la tasa instantánea es igual a la derivada de la función f’(x) dividida por la función f(x), y como la derivada del logaritmo de una función también es igual a la derivada de la función dividida por la función, tendremos:
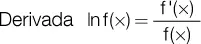
Por lo tanto, la tasa instantánea representa la derivada del logaritmo natural de la función, y la función del monto compuesto es igual a: f(x) = (1 + i) n, que es una función del tipo a x.
Como la derivada de una función a x= a xln a, entonces se demuestra:
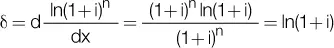
A continuación, se resumen las derivadas de las funciones más utilizadas:
| Si la función es: |
Su derivada es: |
| 1) y = a |
1) y’ = 0 |
| 2) y = x |
2) y’ = 1 |
| 3) y = x n |
3) y’ = n · x n-1 |
| 4) y = a · x n |
4) y’ = a · n · x n-1 |
5) 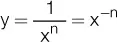 |
5) y’ = (-n) · x -n-1 |
| 6) y = ln x |
6) 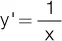 |
| 7) y = a x |
7) y’ = a x· log ea |
| 8) y = e x |
8) y’ = e x |
| 9) y = u · u |
9) y’ = u’ · u + u · u’ |
10) 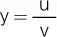 |
10) 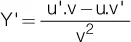 |
| 11) y = u + v |
11) y’ = u’ + v’ |
| 12) y = u − v |
12) y’ = u’ − v’ |
| 13) y = a n |
13) y’ = a n· ln a · n’ |
| 14) y = e u |
14) y’ = e u· u’ |
| 15) y = log eu |
15) 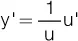 |
1.3 Contenido de la página web de apoyo
El material marcado con asterisco (*) solo está disponible para docentes.
Mapa conceptual
Autoevaluación
Presentaciones*
____________
1 Si el 9,6 % anual compuesto es una buena tasa de rendimiento, todo depende de la inflación que hubo en ese período y de los rendimientos que se alcanzaron con otras inversiones de riesgo similar.
2 El interés compuesto también puede exterminar al deudor. Si hubiéramos recibido 1 millón en préstamo, y nunca hubiéramos amortizado capital o pagado intereses, deberíamos 100 millones al cabo de 50 años.
3 Del otro lado, podría decirse que las empresas que aumentaron sus precios estarían en condiciones de pagar tasas más altas.
Contenido
2.1 Introducción
2.2 Monto a interés simple
2.3 Descuento simple
2.4 Equivalencia de capitales en el régimen simple y reemplazo de pagos
2.5 Resumen
2.6 Preguntas
2.7 Problemas
2.8 Respuesta a las preguntas
2.9 Resolución de los problemas
2.10 Contenido de la página web de apoyo
Objetivos
• Calcular el monto de un depósito a plazo fijo y el interés de la operación.
• Calcular el valor presente en una operación de descuento.
• Calcular una tasa proporcional.
• Calcular un capital equivalente dando un vencimiento común a documentos que vencen en diferentes fechas.
En el contexto del cálculo financiero, es posible hablar de dos tipos de régimen: simple y compuesto. Entendemos por régimen simple aquel donde los intereses se calculan siempre sobre el capital inicial de la operación; por lo tanto, los intereses que produce dicho capital son siempre una suma fija.
Читать дальше

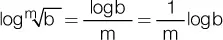
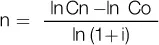
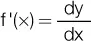 .
.