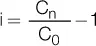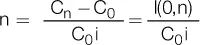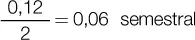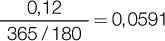Guillermo L. Dumrauf - Manual de matemáticas financieras

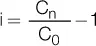
c. Fórmula del número de períodos

Simplemente, observe que el numerador de la fórmula representa el interés acumulado, de forma tal que también puede escribirse:

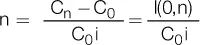
d. Fórmula del interés acumulado

Para un capital inicial de C 0, el valor de I(0,n) representa el valor absoluto del interés acumulado, y estará dado por la relación: I(0,n) = C 0in, que quiere decir que ganamos «n veces la tasa de interés sobre el capital». Por ejemplo, 100 euros colocados durante 10 períodos al 5 % representan un interés acumulado de 50 €:

I(0,10) = 100 × 0,05 × 10 = 50

La fórmula del interés acumulado también puede razonarse como la diferencia entre el monto y el capital inicial:

I(0,n) = C n− C 0= C 0(1 + in) − C 0= C 0+ C 0in − C 0= C 0in

O como la suma de todos los intereses periódicos:

I(0,n) = I(0,1) + I(1,2) + … + I(n − 1,n) = C 0i + C 0i + … C 0i = C 0in

En el régimen simple, las tasas siempre se suman.

e. Fórmula del monto a interés simple cuando cambia la tasa de interés y rigen por períodos irregulares

En la práctica, la tasa de interés no es constante, y también es posible que cada tasa se gane por períodos de tiempo diferentes; en este caso, no podemos utilizar la fórmula genérica del interés simple, puesto que la tasa es posible que se haya modificado mensualmente. En ese caso, desarrollaremos un factor de capitalización sumando las distintas tasas i 1, i 2... i n, para los diferentes períodos de tiempo, (en el caso de que sean diferentes, los llamaremos p 1, p 2... p n). La fórmula resultante es:

C n= C 0(1 + i 1p 1+ i 2p 2+ ... + i np n)

Ejemplo 1: se depositaron 100 € durante 3 meses con las siguientes tasas de interés: primer mes = 2 %; segundo mes = 4 %; tercer mes: 6 %. Se desea saber el monto de la operación:

Cn = 100 (1 + 0,02 + 0,04 + 0,06) = 112

Ejemplo 2: se depositaron 100 € durante 3,5 meses con las siguientes tasas de interés: primer mes = 2 %; segundo mes = 4 %; por los últimos 45 días se obtuvo el 6 % mensual. Se desea saber el monto de la operación:

C n= 100 (1 + 0,02 + 0,04 + 0,06 × 1,5) = 115

En la práctica, es común que se realicen operaciones de plazo fijo pactando una tasa nominal que llamaremos j(m), pero que los intereses capitalicen en forma subperiódica; en ese caso, debemos proporcionar la tasa nominal en el momento en el que capitalizan los intereses. 2 La tasa nominal es solo la tasa de pacto de la operación, sirve como referencia para el cálculo de la tasa efectiva de la operación. Así, es posible tener una tasa nominal anual, pero que capitaliza semestralmente, es decir, los interés se capitalizan a los seis meses, antes de llegar al año. Para obtener la tasa proporcional, simplemente dividimos la tasa nominal por el número de subperíodos de capitalización; que denominamos m:

Un punto importante es que la tasa proporcional obtenida a partir del dato de la tasa nominal es, a la vez, una tasa efectiva para el período de capitalización considerado; por ejemplo, una tasa nominal anual del 12 % que capitaliza semestralmente, arroja una tasa semestral del 6 %, que es a la vez una tasa efectiva y proporcional, pues representa el rendimiento que efectivamente se obtuvo al cabo de un semestre:

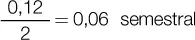
Resumiendo, la diferencia importante entre la tasa nominal y la tasa proporcional subperiódica es la no coincidencia de la unidad de tiempo en que está expresada la tasa de interés (nominal) con el período de capitalización. Otro detalle por observar es que, en el régimen simple, las tasas son al mismo tiempo proporcionales y equivalentes. Recuerde que en el interés simple las tasas se suman, de forma tal que da lo mismo ganar un 6 % en un semestre que el 12 % en el año. En el próximo capítulo veremos que no es lo mismo en el régimen compuesto, donde las tasas son solamente «equivalentes».

En algunos contratos de operaciones financieras, dependiendo de la legislación de cada país, se utiliza el año civil de 365 días, por lo que la tasa proporcional que resulta es ligeramente menor que la que obtendríamos con un año de 360 días; por ejemplo, para el caso anterior la tasa de 180 días sería:

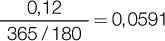
En la práctica, el cálculo suele hacerse como 0,12 × 180 / 365, que resulta más rápido cuando se utiliza una calculadora de bolsillo. La consideración de los días contenidos en el año nos lleva al tema del interés exacto.

Los mercados financieros exhiben algunas discrepancias con respecto a la forma en que se consideran los días que contiene el año. En algunos contratos, se utilizan 360 días en lugar de los 365 días que el año contiene. De esta forma, podemos distinguir:

• Año exacto o civil: cuando se toman 365 días

• Año comercial: cuando se toman 360 días

Ejemplo: calcular el interés que se obtuvo en una operación donde se depositó un capital de 10.000 € durante 180 días, ganando una tasa nominal anual del 12 %. Resolver por año civil y por año comercial.

El interés obtenido utilizando el año comercial resulta un poco mayor que el obtenido utilizando el año civil, debido a que el resultado del cociente es un poco mayor al dividir por 360 en lugar de dividir por 365. Para conocer la relación entre los dos, simplemente dividimos miembro a miembro las relaciones indicadas anteriormente:

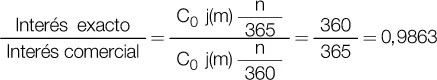
Y observamos que el interés exacto es un 98,63 % del interés comercial:

Interés exacto Interés comercial 0,9863

a. Los depósitos a plazo

Los certificados depósito a plazo fijo son instrumentos que especifican capitales, plazos y tasas de interés. Habitualmente no se negocian, si bien la reforma reciente del Código Civil y Comercial de la Nación lo permite (consulte la normativa vigente en su país), y existen en general plazos mínimos de tiempo por los cuales pueden constituirse, de forma tal que su liquidez es menor que una cuenta de ahorros. Cuando hacemos un plazo fijo inmovilizamos el dinero por el período de contrato (no importa el plazo, siempre es un solo período de 30, 45, 60 o más días, ya que no hay capitalización de intereses); por lo tanto, la operación se realiza dentro de las reglas del interés simple. La capitalización solo se produciría si se renovara la operación, pero entonces habría más de un período.