Using those limits gives
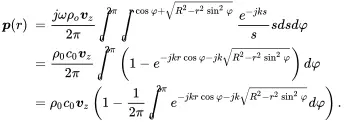 (2.149)
(2.149)
Inserting equation ( 2.149) into ( 2.146) leads to the expression
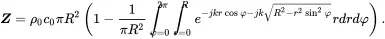 (2.150)
(2.150)
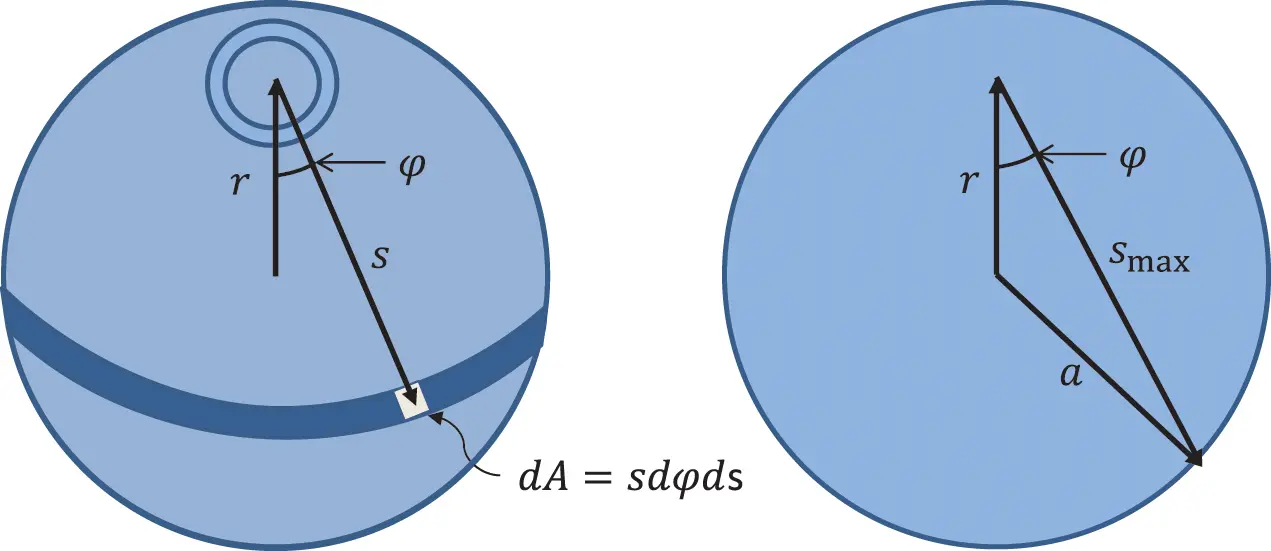
Figure 2.13Surface integration over piston for radiation impedance. Source : Alexander Peiffer.
Running through quite a lot of algebraic modifications we get the expression for the impedance of a piston
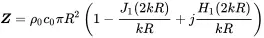 (2.151)
(2.151)
or
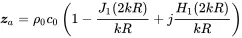 (2.152)
(2.152)
H1(z) is the Hankel function of first order. In Figure 2.14 the real and imaginary parts of the acoustic radiation impedance are compared to those of the pulsating sphere. Both sources have a similar shape except some waviness for the piston resulting from interference effects from the integration over the piston surface. For large kR the impedance is real for both radiators and approaches the acoustic impedance of a plane wave z0=ρ0c0.
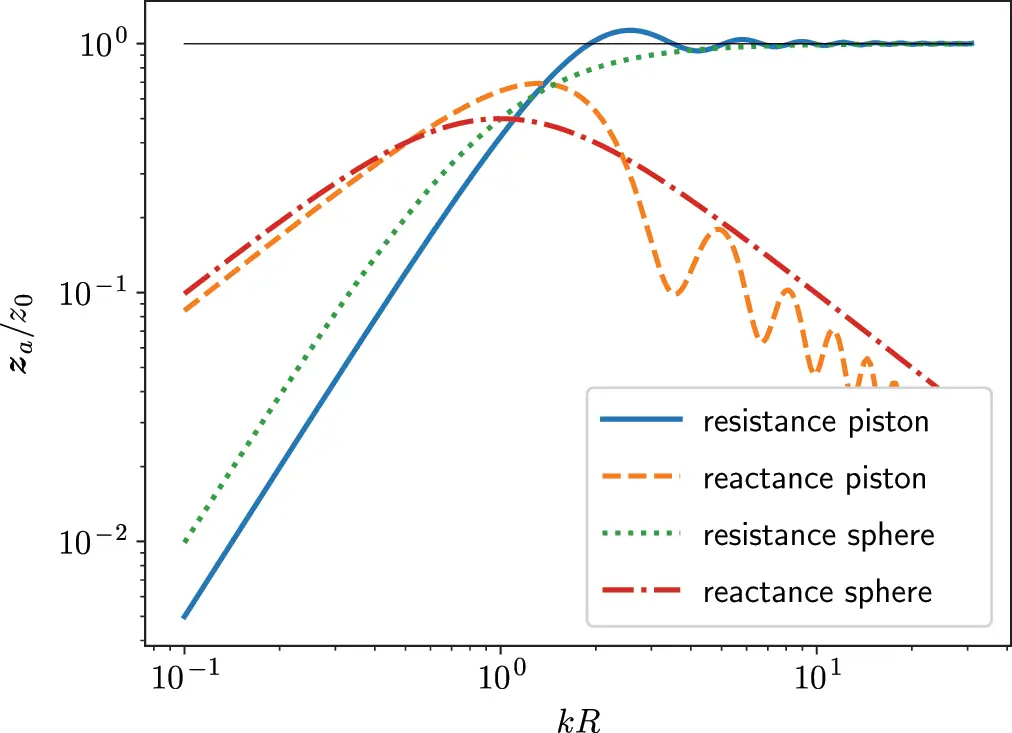
Figure 2.14 Acoustic radiation impedance of the piston. Source : Alexander Peiffer.
With Equation ( 2.87) the radiated power of a piston of source strength Q=πR2vz is
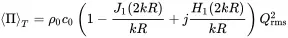 (2.153)
(2.153)
The main use of Equation ( 2.153) is that the required velocity to achieve (or prevent) a certain sound power can be calculated from it, for example if one must define the boundary condition for a radiating piston in simulation software and only the radiated power is known.
The Bessel functions can be approximated by a series in 2kR taking the first series term of both functions (Jacobsen, 2011)
 (2.154)
(2.154)
This expression is valid for ka<0.5. From the imaginary part we get for the mass
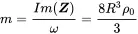 (2.155)
(2.155)
Assuming a cylindrical volume V=πR2lc of the fluid above the piston we can calculate the length of the moving mass cylinder to be
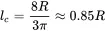 (2.156)
(2.156)
meaning that at low frequencies the piston is moving a fluid layer of 0.85 times the radius acting as an inertia without radiation.
For the radiated power calculation of the piston we took the pressure at the piston surface and integrated the pressure–velocity product over the surface. Due to the fact that the velocity is constant the surface integral involves mainly the pressure as a space-dependent property. In case of vibrating structures with complex shapes of vibration the velocity distribution over the surface is not homogeneous, and we need a more detailed approach.
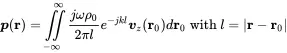 (2.157)
(2.157)
In the above equation a function with argument (r−r0) is multiplied by the velocity function for r0 and integrated over the two-dimensional space. Mathematically, this can be interpreted as a two-dimensional convolution in space
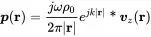 (2.158)
(2.158)
Thus, when we apply the two-dimensional Fourier transform to the Rayleigh integral the result is the product of the Fourier transform of the vibration shape vz(r0) and the Green’s function in wavenumber space leading to
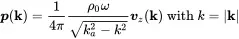 (2.159)
(2.159)
So, we have replaced the expensive convolution operation by a multiplication. This simplification is at the cost of two-dimensional Fourier transforms that are required to get the expressions in wavenumber domain.
The time averaged intensity of a sound field is given by the product of pressure and velocity ( 2.45). As the velocity is not uniform over the surface we perform a surface integration over the vibrating area to get the total radiated power
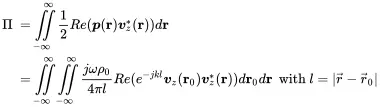 (2.160)
(2.160)
Thus, for the determination of radiated power a double area integral is required that may become computationally expensive.
In the above expression we can also switch to the wavenumber domain. In this case the area integration is replaced by an integration over the two-dimensional wavenumber space.
 (2.161)
(2.161)
The double integral is replaced by a single two-dimensional wavenumber integration. Thus, once the shape function is available the power calculation in wavenumber space is much faster than in real space (Graham, 1996).
2.7.4.1 Radiation Efficiency
The radiation efficiency is a quantity that relates the power of a plane wave to the radiated power of a vibrating surface with same surface averaged velocity. The definition of the radiation efficiency was motivated by experimental procedures because it allows the estimation of the radiated power from the measurements of the vibration velocity. The squared average velocity of a vibrating surface is
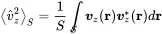 (2.162)
(2.162)
and the power radiated by a plane wave through the same area S is given by ( 2.47)
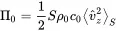 (2.163)
(2.163)
The radiation efficiency is defined as the ratio between the radiated power of a velocity profile vz(r) of a surface S and the standardized power of the plane wave:
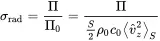 (2.164)
(2.164)
Читать дальше

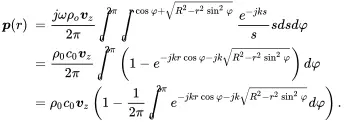 (2.149)
(2.149)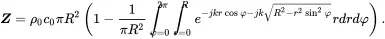 (2.150)
(2.150)
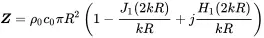 (2.151)
(2.151)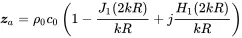 (2.152)
(2.152)
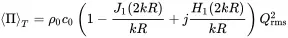 (2.153)
(2.153) (2.154)
(2.154)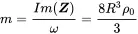 (2.155)
(2.155)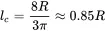 (2.156)
(2.156)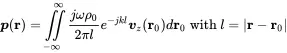 (2.157)
(2.157)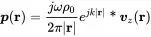 (2.158)
(2.158)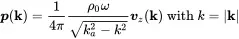 (2.159)
(2.159)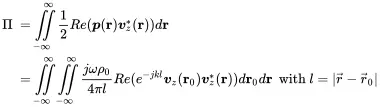 (2.160)
(2.160) (2.161)
(2.161)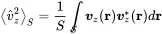 (2.162)
(2.162)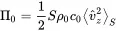 (2.163)
(2.163)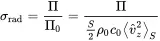 (2.164)
(2.164)










