Here α is the damping constant. There are several reasons for the attenuation of acoustic waves:
Viscous damping due to inner viscosity.
Thermal damping due to irreversible heat flow during wave propagation.
Molecular damping due to excitation of degrees of freedom of molecules (for additional content of the gas, e.g. humidity in air).
The damping loss η as defined in (1.68) is based on the amount of energy dissipated during one cycle of wave motion. The harmonic pressure wave performs one cycle of oscillation in one period in time T or space λ. So we get for η:
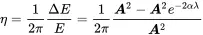 (2.56)
(2.56)
For small damping the exponential function can be approximated by ex≈1+x−… providing the relationship between damping loss and fluid wave attenuation.
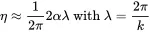 (2.57)
(2.57)
Hence, the attenuation can be given by:
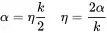 (2.58)
(2.58)
An appropriate way to consider this relationship in the solution of the wave equation is to include this into a complex wavenumber k:
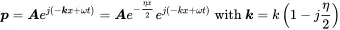 (2.59)
(2.59)
This complex wavenumber naturally impacts the speed of sound
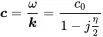 (2.60)
(2.60)
and the acoustic impedance
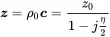 (2.61)
(2.61)
The shown quantities of the plane wave field can also be applied in three-dimensional space and they are summarized in Table 2.2.
Table 2.2 Field and energy properties of acoustic waves.
| Quantity |
Symbol |
Formula |
Units |
Plane wave |
Equation |
| Acoustic velocity |
v |
1jωc0∇p |
m/s |
pρ0c0 |
( 2.35) |
| Acoustic impedance |
z |
p/v |
Pa s/m |
z0=ρ0c0 |
( 2.38) |
| Intensity |
I |
12Re(pv*) |
Pa m/s |
⟨I⟩T=p^22ρ0c0 |
( 2.47) |
| Energy density |
e |
|
J/m 3 |
⟨e⟩T=p^22ρ0c02 |
( 2.52) |
| Acoustic power |
Π |
Π=IA |
W |
⟨Π⟩T=Ap^22ρ0c0 |
( 2.43) |
2.4 Fundamental Acoustic Sources
The radiation of sound is key to understanding how energy is introduced into wave fields. Depending on the wavelength, geometry, and dimension of the source the behavior varies. A detailed understanding of fundamental sources is helpful for the radiation of vibrating structures and thus, how they exchange acoustic energy.
2.4.1 Monopoles – Spherical Sources
The most simple geometry we might think of is a point in space. For simple derivation of the sound field of a point source the spherical coordinate system is introduced as shown in Figure 2.4 and defined by the following coordinate transformation
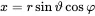 (2.62a)
(2.62a)
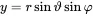 (2.62b)
(2.62b)
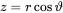 (2.62c)
(2.62c)
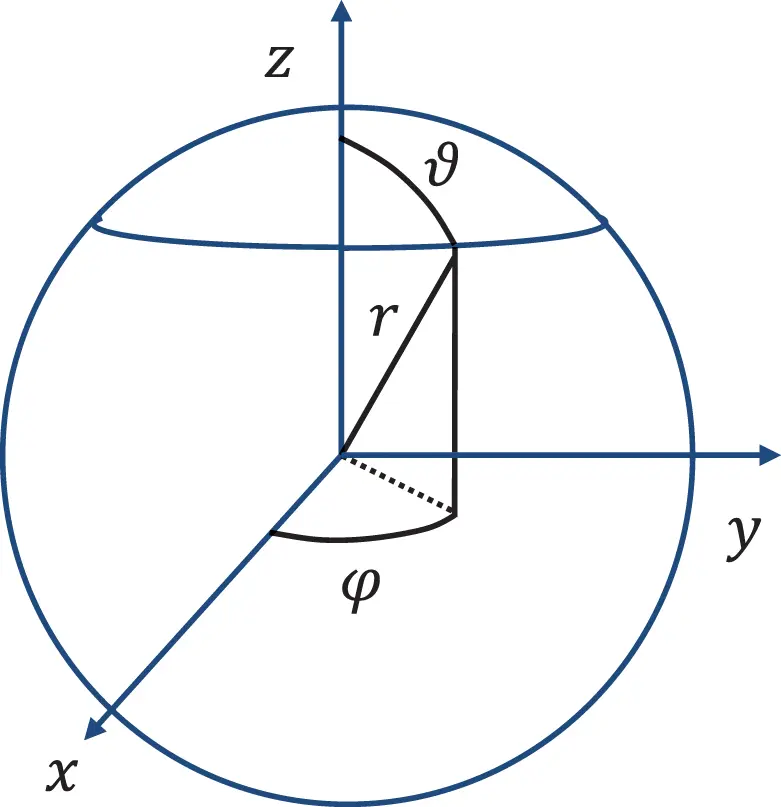
Figure 2.4 Definition of a spherical coordinate system. Source : Alexander Peiffer.
Using this coordinate system and neglecting the angular components the Laplace operator Δ reads as
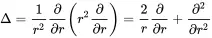 (2.63)
(2.63)
The wave equation for the velocity potential ( 2.30) becomes
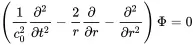 (2.64)
(2.64)
The two right terms can be written in a different form using rΦ as argument
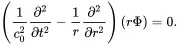 (2.65)
(2.65)
Equation ( 2.30) is the one-dimensional wave equation for the argument rΦ, so we can use the D’Alambert solution
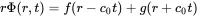 (2.66)
(2.66)
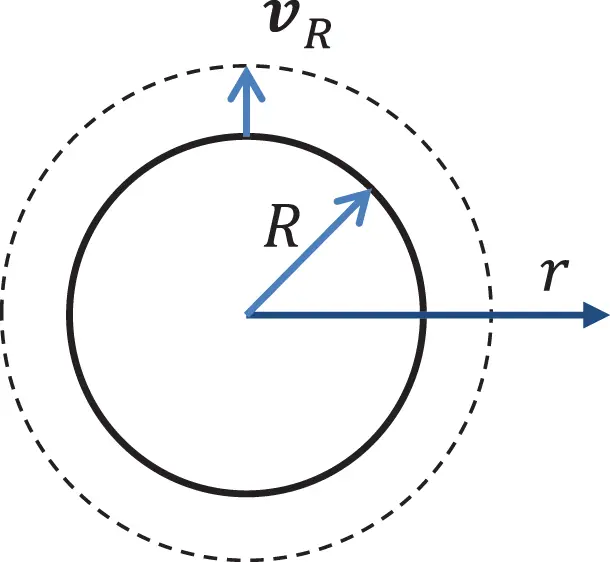
Figure 2.5Breathing sphere as source model for a monopole. Source : Alexander Peiffer.
The first term represents an outgoing wave travelling away from the source, the second an incoming wave travelling to the source. As we are interested in sound being emitted from the source we consider the outgoing harmonic solution with complex amplitude A
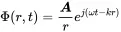 (2.67)
(2.67)
Consider a pulsating sphere of radius R in the centre with normal surface velocity vR. With the velocity potential the radial velocity can be easily derived from the solution ( 2.67):
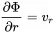 (2.68)
(2.68)
Substituting Equation ( 2.67) into ( 2.68) and solving for A gives
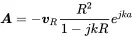 (2.69)
(2.69)
Hence,
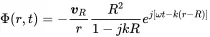 (2.70)
(2.70)
The strength Q(t) of the source is defined by the volume flow rate. This is the surface of the sphere times normal velocity vR
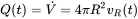 (2.71)
(2.71)
With the harmonic source strength
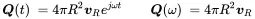 (2.72)
(2.72)
the spherical wave solution is
Читать дальше

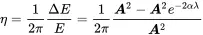 (2.56)
(2.56)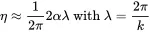 (2.57)
(2.57)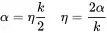 (2.58)
(2.58)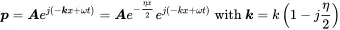 (2.59)
(2.59)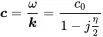 (2.60)
(2.60)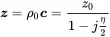 (2.61)
(2.61)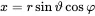 (2.62a)
(2.62a)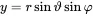 (2.62b)
(2.62b)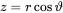 (2.62c)
(2.62c)
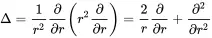 (2.63)
(2.63)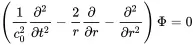 (2.64)
(2.64)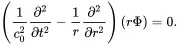 (2.65)
(2.65)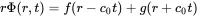 (2.66)
(2.66)
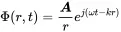 (2.67)
(2.67)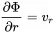 (2.68)
(2.68)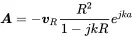 (2.69)
(2.69)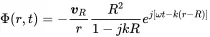 (2.70)
(2.70)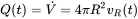 (2.71)
(2.71)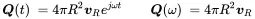 (2.72)
(2.72)










