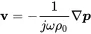 (2.35)
(2.35)
For one-dimensional waves in the x-direction this leads to:
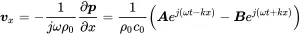 (2.36)
(2.36)
Depending on the wave orientation the ratio between pressure and velocity is given by:
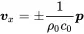 (2.37)
(2.37)
In accordance with the impedance concept from section 1.2.3 we define the ratio of complex pressure and velocity as specific acoustic impedance z
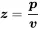 (2.38)
(2.38)
also called acoustic impedance. For plane waves this leads to:
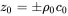 (2.39)
(2.39)
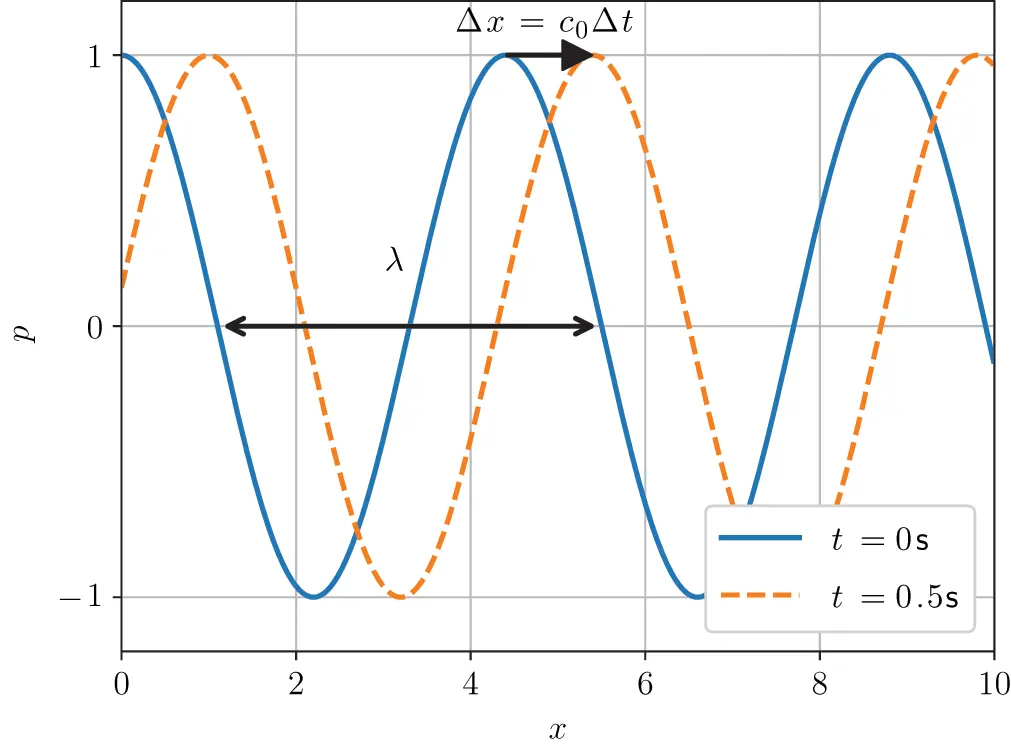
Figure 2.3One-dimensional harmonic waves travelling in the positive x-direction (c0=2m/s, T=2.2s). Source : Alexander Peiffer.
z0=ρ0c0 is called the characteristic acoustic impedance of the fluid. The specific acoustic impedance z is complex, because for waves that are not plane the velocity may be out of phase with the pressure. However, for plane waves the specific acoustic impedance is real and an important fluid property.
The above description of plane waves can be extended to three-dimensional space by introducing a wavenumber vector k.
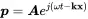 (2.40)
(2.40)
Entering ( 2.40) into the wave Equation ( 2.27) provides
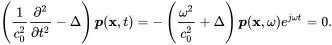 (2.41)
(2.41)
The ejωt term is often omitted and with k=ω/c0 we get the homogeneous.
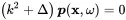 (2.42)
(2.42)
2.3.3 Field Quantities: Sound Intensity, Energy Density and Sound Power
A sound wave carries a certain amount of energy that is moving with the speed of sound. We start with the instantaneous acoustic power Π:
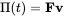 (2.43)
(2.43)
F is the force acting on a fluid particle and v the associated velocity. The acoustic intensity I is defined as the power per unit area A=An in the direction of the unit vector n and with F=pAn we get:
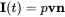 (2.44)
(2.44)
As in Equation (1.48) the time average is given by:
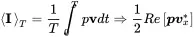 (2.45)
(2.45)
Using the harmonic plane wave solutions for pressure ( 2.34) and velocity ( 2.36)
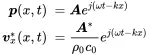
the time averaged mean intensity yields:
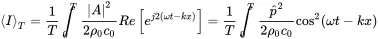 (2.46)
(2.46)
and finally:
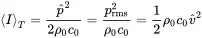 (2.47)
(2.47)
We see that the specific impedance z0=ρ0c0 relates the intensity to the squared pressure.
The kinetic energy density ekin in a control volume V0 is written as
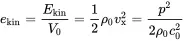 (2.48)
(2.48)
The potential energy density epot follows from the adiabatic work integral as in equation ( 2.9)
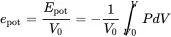 (2.49)
(2.49)
If we use Equation ( 2.15) we get the change in density as a start for the change in volume
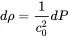
With unit mass M in the control volume V0 it follows from ρ=M/V0 that
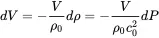
Finally we get:
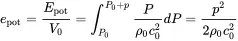 (2.50)
(2.50)
Pressure and velocity are in phase for plane waves; the same is true for the potential and kinetic energy density, so the total energy density is given by:
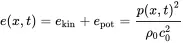 (2.51)
(2.51)
Using Equation ( 2.34) the time average over one period leads to:
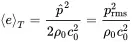 (2.52)
(2.52)
Finally, we can see that the speed of sound relates energy density to the sound intensity.
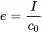 (2.53)
(2.53)
All those above expressions are useful for the description and evaluation of sound fields. Especially in case of statistical methods that are based on the energy density of acoustic subsystems they link the wave fields to the energy in the systems and the power irradiating at the system boundaries.
If the intensity can be determined over a certain surface the source power is calculated by integrating the intensity component perpendicular to the surface
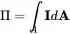 (2.54)
(2.54)
There is no motion without damping, and a sound wave propagating over a long distance will vanish. This is considered by adding a damping component to the one-dimensional solution of the wave equation similar to the decay rate in (1.22)
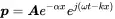 (2.55)
(2.55)
Читать дальше

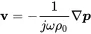 (2.35)
(2.35)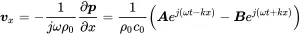 (2.36)
(2.36)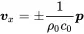 (2.37)
(2.37)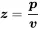 (2.38)
(2.38)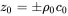 (2.39)
(2.39)
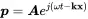 (2.40)
(2.40)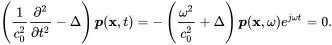 (2.41)
(2.41)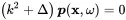 (2.42)
(2.42)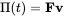 (2.43)
(2.43)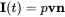 (2.44)
(2.44)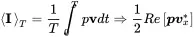 (2.45)
(2.45)
 (2.46)
(2.46) (2.47)
(2.47) (2.48)
(2.48)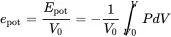 (2.49)
(2.49)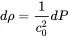
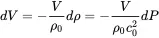
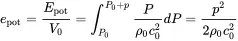 (2.50)
(2.50)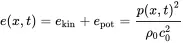 (2.51)
(2.51)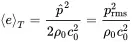 (2.52)
(2.52)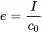 (2.53)
(2.53)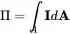 (2.54)
(2.54)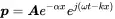 (2.55)
(2.55)










