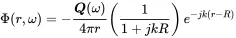 (2.73)
(2.73)
Using equations ( 2.25) and ( 2.35) pressure and velocity are given by
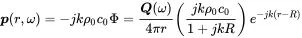 (2.74)
(2.74)
and
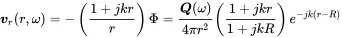 (2.75)
(2.75)
2.4.1.1 Field Properties of Spherical Waves
The acoustic impedance z is according to Equation ( 2.38)
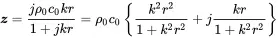 (2.76)
(2.76)
In contrast to the plane wave, the specific acoustic impedance is not real. It contains a resistive and a reactive part. When the resistive part is dominant the pressure is in phase with the velocity. When the reactive part dominates, the velocity is out of phase to the pressure. The out of phase component does not generate any power in the sound field as it was the case for moving a mass or driving a spring. The motion is partly introduced into the local kinetic energy, and this part can be recovered as it is the case for an oscillating mass. For the acoustic field of a spherical source the reactive field represents the near-field fluid volume that is carried by the sphere motion but not emitting a wave.
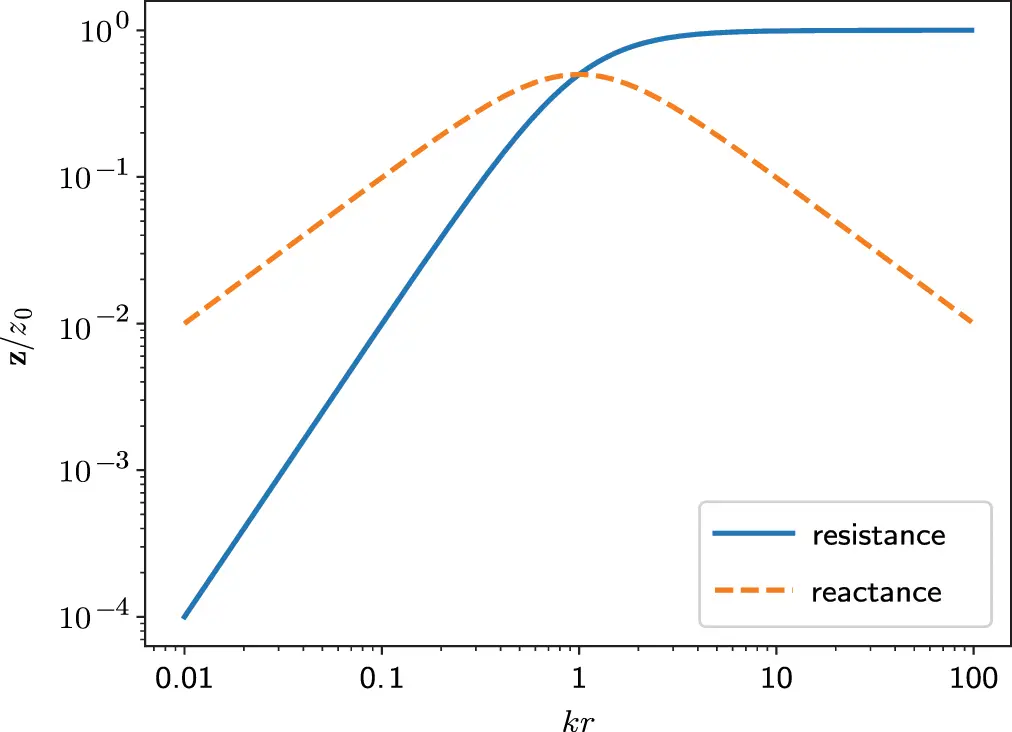
Figure 2.6Reactance and resistance of specific acoustic impedance of a pulsating sphere. Source : Alexander Peiffer.
There are two limit cases in Equation ( 2.76):
1 kr≪1; the wave length λ is much larger than distance r.
2 kr≫1; the wave length λ is much smaller than distance r.
Introducing the above approximations into Equation ( 2.76) gives a fully reactive impedance for (i)
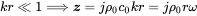 (2.77)
(2.77)
and a resistive part equal to plane waves for (ii)
 (2.78)
(2.78)
2.4.1.2 Field Intensity, Power and Source Strength
The time averaged radiated intensity is
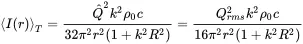 (2.79)
(2.79)
The total radiated power can now be evaluated from Equation ( 2.54) and the integration surface 4πr2
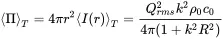 (2.80)
(2.80)
The mean square pressure can be derived from ( 2.74) and expressed by the intensity using ( 2.45)
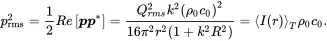 (2.81)
(2.81)
Replacing the intensity in ( 2.81) gives the rms pressure in the spherical sound field due to power
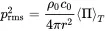 (2.82)
(2.82)
2.4.1.3 Power and Radiation Impedance at the Surface Sphere
The characteristic impedance of the sphere exactly at the surface at radius R can be translated into the radiation impedance of the sphere as a volume source. The radiation impedance is defined as the ratio of pressure to source strength at the vibrating surface
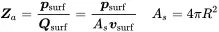 (2.83)
(2.83)
If we assume a constant harmonic surface velocity vR we get for the radiation impedance of the breathing sphere and according to the acoustic impedance ( 2.76)
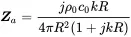 (2.84)
(2.84)
The acoustic radiation impedance is the ratio pressure and normal velocity at the sphere’s surface
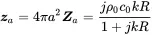 (2.85)
(2.85)
We can now use this impedance to eliminate either p or vr. The power transmitted by a vibrating sphere using Equation ( 2.54) over the surface of the sphere
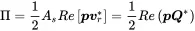 (2.86)
(2.86)
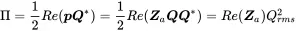 (2.87)
(2.87)
or for constant source pressure
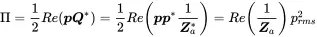 (2.88)
(2.88)
It is instructive to see the mechanical properties considering the limit cases from above and extract the mass that is moved by the surface. From Newtons’s law a force given by F=4πR2p leads to an in-phase acceleration of jωvr of a mass m
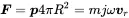
hence
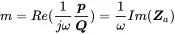 (2.89)
(2.89)
For kR≪1 we get: m=4πR3ρ0=3Vsphρ0. Thus, at low frequencies the source surface motion carries three times the fluid volume of the sphere. This motion near the source is called an evanescent wave, because it is oscillatory motion of fluid that does not radiate.
A point source is a spherical source with an infinitely small radius. Performing the limit kR→0 for Equation ( 2.73) leads to the velocity potential for point sources of strength Q
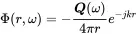 (2.90)
(2.90)
The pressure and velocity field of such a source is given by
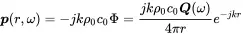 (2.91)
(2.91)
and
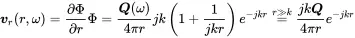 (2.92)
(2.92)
All other relations regarding power and intensity expressions remain. We see that the limit is expressed for kR and not for the wavelength. The reason is that it is the ratio of a characteristic length (in this case the sphere radius) to the wavelength that determines if the geometrical details must be considered or not. In other words, a wave of a certain wavelength doesn’t care about details that are much smaller.
Читать дальше

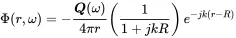 (2.73)
(2.73)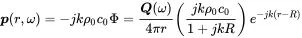 (2.74)
(2.74)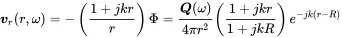 (2.75)
(2.75)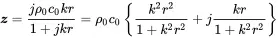 (2.76)
(2.76)
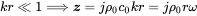 (2.77)
(2.77) (2.78)
(2.78)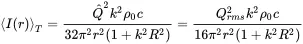 (2.79)
(2.79)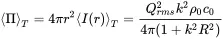 (2.80)
(2.80)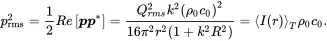 (2.81)
(2.81)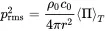 (2.82)
(2.82)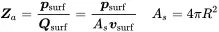 (2.83)
(2.83)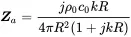 (2.84)
(2.84)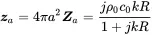 (2.85)
(2.85)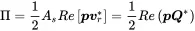 (2.86)
(2.86)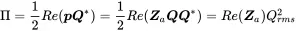 (2.87)
(2.87)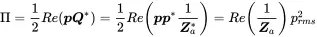 (2.88)
(2.88)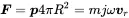
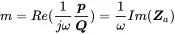 (2.89)
(2.89)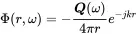 (2.90)
(2.90)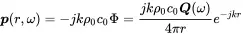 (2.91)
(2.91)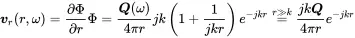 (2.92)
(2.92)










