Exchanging r and r0 and integrating r0 over the volume V gives
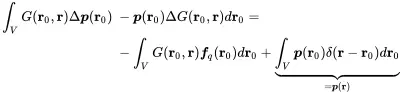 (2.134)
(2.134)
The last term on the RHS follows from the sifting property of the delta function
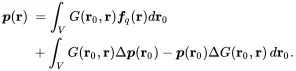 (2.135)
(2.135)
With Green’s law of vector analysis
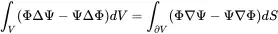 (2.136)
(2.136)
some volume integrals can be transferred into surface integrals and we get finally
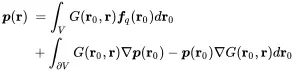 (2.137)
(2.137)
The first term on the right-hand side is the volume integral over all sources fq(r) in the volume. So given a known source distribution we can calculate the according sound field. The two terms in the surface integral take care of the boundary condition. The pressure gradient in the first can be converted into the normal velocity using ( 2.35). The second surface integral allows establishing the correct surface impedance. Equation ( 2.137) is called the constant frequency version of the .
The Rayleigh integral is a special solution of the Kirchhoff-Helmholtz integral applied to flat and infinite surfaces. We assume a configuration as shown in Figure 2.10. The integration volume is the right half space for z>0 closed by a half sphere of infinite radius. The Green’s function of any source at r0=(x0,y0,z0) with z0>0 is as defined in equation ( 2.127). The rigid surface acts as a reflector. Thus, there is a mirror source located at r0′=(x0,y0,−z0). This source is not in volume V, and the added wave field is therefore considered as a homogeneous solution in the volume. Hence, we get for the generalized Green’s function
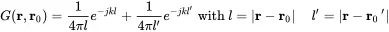 (2.138)
(2.138)
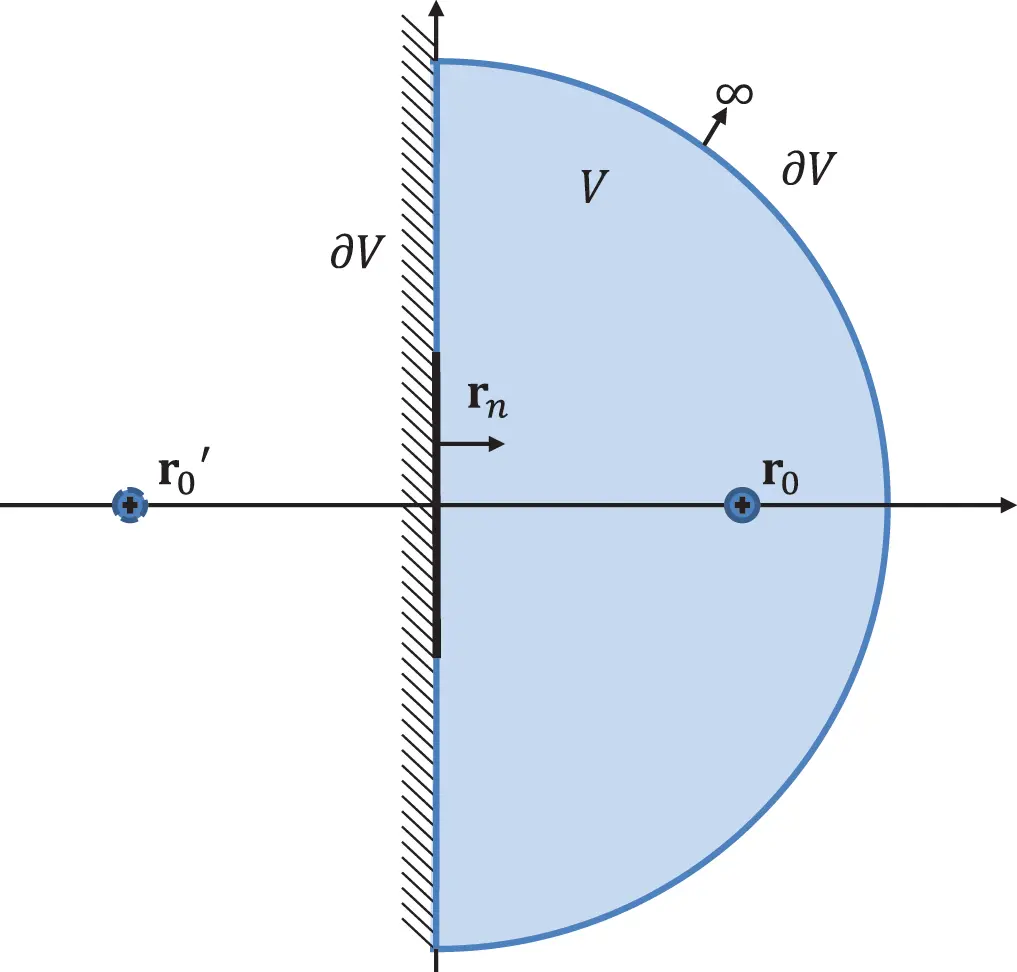
Figure 2.10 Half space in front of a rigid wall. Source : Alexander Peiffer.
We enter this version of the Green’s function in Equation ( 2.137) and we get
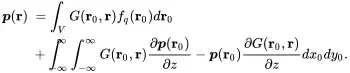 (2.139)
(2.139)
We assume a source-free half space so fq(r)=0, and due to the mirror source symmetry ∂G(r0,r)∂z=0 is also true. By clever selection of the Green’s function we fulfilled the boundary condition automatically. For the surface integral the contributions from the half sphere with infinite radius are supposed to be zero. From Equation ( 2.35) the first expression can be converted into an expression for the surface velocity vz. Performing the limit process z0→0 we get
 (2.140)
(2.140)
and with this Green’s function we can derive the Rayleigh integral that allows the calculation of infinite half space sound fields excited by a rigid vibrating plane with arbitrary velocity distribution vz(x0,y0).
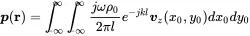 (2.141)
(2.141)
A cylindrical loudspeaker in a wall can be modelled by a piston of radius R vibrating with velocity vz located in a rigid wall. For convenience the surface integral will be expressed in cylindrical coordinates r0 and φ0. The receiver coordinates are given as spherical coordinates r and ϑ(Figure 2.11). Without loss of generality the azimuthal angle φ is set to zero.
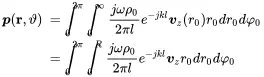 (2.142)
(2.142)
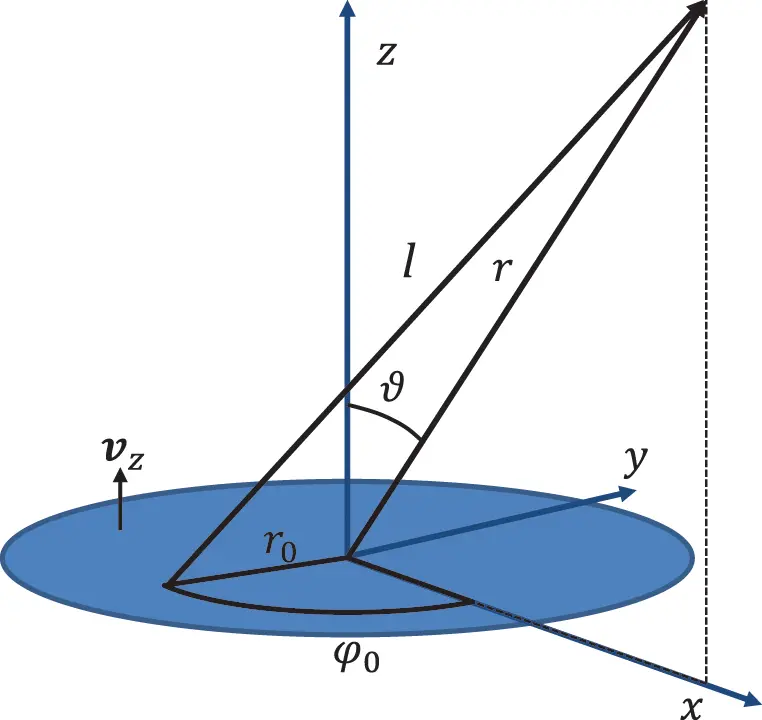
Figure 2.11 Coordinate definitions for the piston in the wall. Source : Alexander Peiffer.
In the far field approximation we assume l≈r and get
 (2.143)
(2.143)
So, the approximate result is
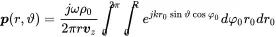 (2.144)
(2.144)
The integral is the Bessel function of first order
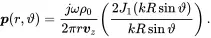 (2.145)
(2.145)
The results for some values of kR are shown in Figure 2.12 over the angular range of ±π/2. For a piston size small compared to the wavelength (kR≤1) the radiation pattern is similar to a point source. The smaller the wavelength gets in relation to the piston radius R the more a specific radiation pattern develops.
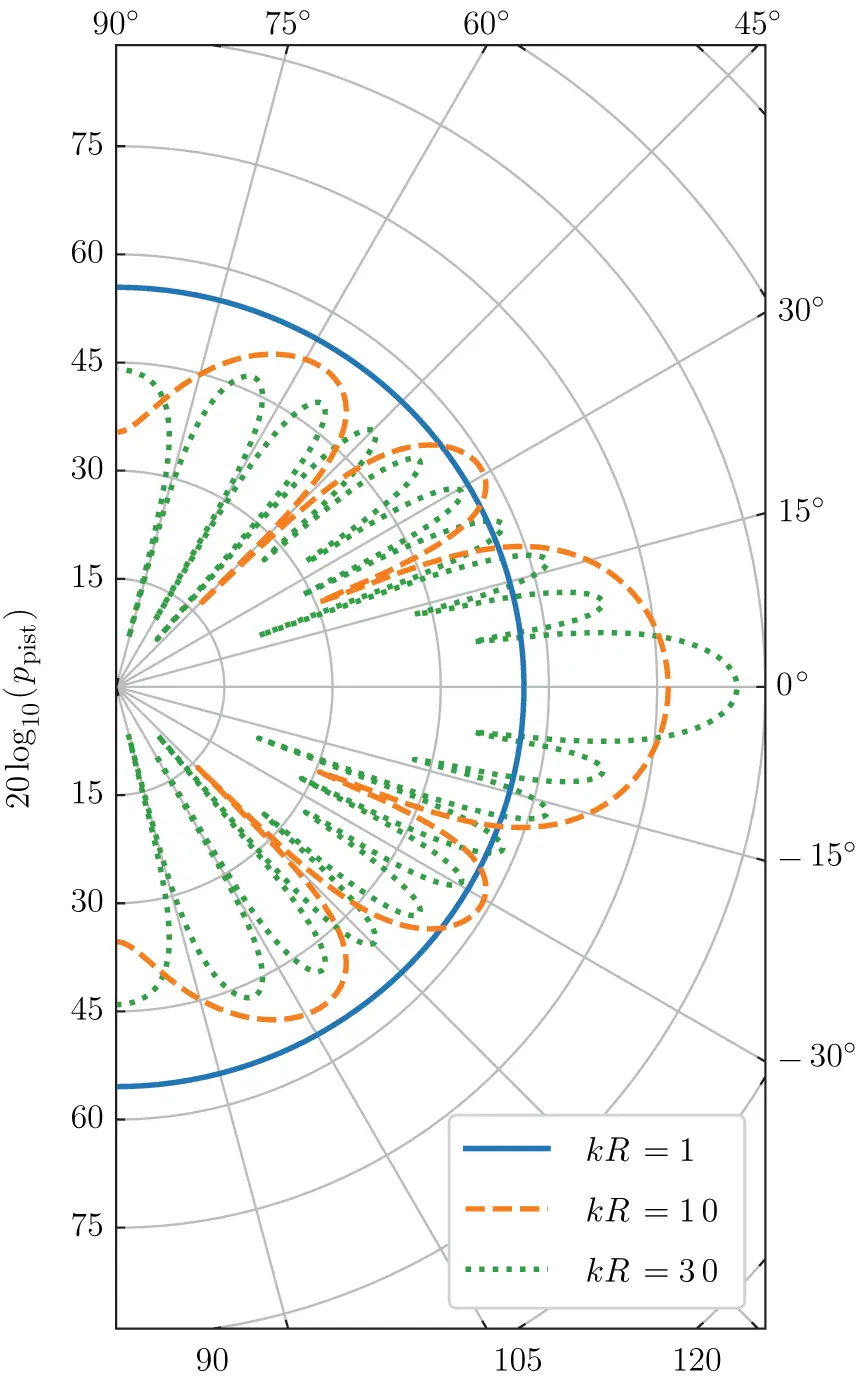
Figure 2.12 Angular distribution (radiation pattern) of the pressure field of the piston. Source : Alexander Peiffer.
2.7.3.1 Impedance Concept
The radiation impedance of the piston is calculated from the pressure averaged over the surface related to the piston velocity vz. As shown by Lerch and Landes (2012) the mechanical impedance of the piston due to radiation is given by
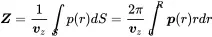 (2.146)
(2.146)
According to equation ( 2.141) assuming a constant velocity vz over the surface A the pressure is
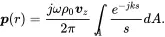 (2.147)
(2.147)
Thus, we get the pressure at r from integrating the contribution from the rest of the piston in circles of radius s. The angle integration over φ0 runs from 0 to 2π. From every angle φ0 follows the integration limits smax of the second integral.
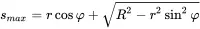 (2.148)
(2.148)
Читать дальше

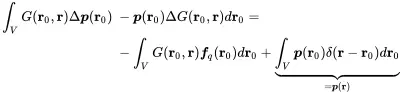 (2.134)
(2.134)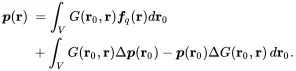 (2.135)
(2.135)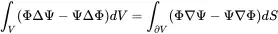 (2.136)
(2.136)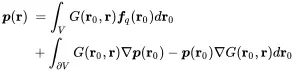 (2.137)
(2.137)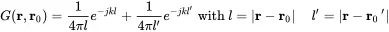 (2.138)
(2.138)
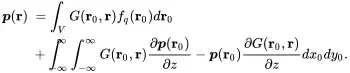 (2.139)
(2.139) (2.140)
(2.140)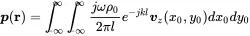 (2.141)
(2.141)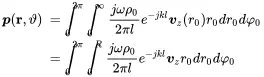 (2.142)
(2.142)
 (2.143)
(2.143)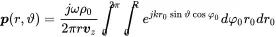 (2.144)
(2.144)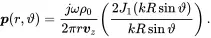 (2.145)
(2.145)
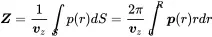 (2.146)
(2.146)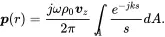 (2.147)
(2.147)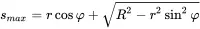 (2.148)
(2.148)










