Нихиль Будума - Основы глубокого обучения

Даже если на сетчатку поступает искаженный вариант цифры, мозг все равно способен воссоздать серию активаций (например, код или плотное векторное представление), которую мы обычно используем для представления изображения этого символа. Это свойство можно попробовать воссоздать в алгоритме для плотного векторного представления. Оно впервые было исследовано Паскалем Винсентом и его коллегами в 2008 году, когда они представили шумопонижающий автокодер [74].

Основные принципы шумопонижения просты. Мы искажаем определенный процент пикселов входного изображения, назначая им нулевое значение. Если исходное изображение — X , искаженный вариант назовем C(X) . Шумопонижающий автокодер идентичен обычному, за исключением одной детали: в его сеть поступает искаженное изображение C(X) , а не X . Автокодер вынужден обучаться для каждого входящего изображения коду, устойчивому к механизму искажения и способному строить интерполяции отсутствующей информации, воссоздавая неповрежденное изображение.

Этот процесс можно представить и геометрически. Допустим, у нас есть двумерный набор данных с разными метками. Возьмем все точки данных в определенной категории (например, с фиксированной меткой) и назовем их S . Любое произвольное семплирование точек может вылиться в любую форму визуализации, но мы предполагаем, что для реальных категорий есть системообразующие структуры, объединяющие все точки S . И они называются многообразием .

Многообразие — форма, которую мы хотим сохранить при уменьшении размерности данных; как писали в 2013 году Ален и Бенджо [75], автокодер неявно усваивает его, обучаясь воссоздавать данные после их прохождения через узкое место нейронной сети (слой кода). Автокодер может понять, к какому из многообразий принадлежит точка, проводя реконструкцию для случая с потенциально разными метками.

Рассмотрим сценарий с рис. 6.13, где точки S — простое малоразмерное многообразие (здесь окружность, выделенная черным). На рис. А мы видим точки данных в S , помеченные черными крестиками, и многообразие, которое оптимально их описывает. Также мы видим аппроксимацию нашей операции искажения.

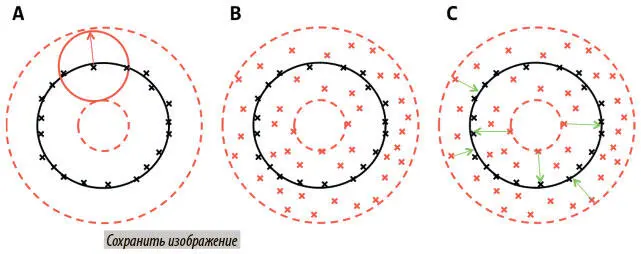
Рис. 6.13. Шумопонижение позволяет модели обучиться многообразию (черная окружность), поняв, как соотнести поврежденные данные (красные крестики) с неповрежденными (черные крестики) при минимизации ошибок (зеленые стрелки) между их представлениями

Красная стрелка и сплошная красная окружность показывают все пути, которыми искажение могло изменить точку данных. Поскольку мы применяем его к каждой точке (на всем многообразии), она искусственно расширяет набор данных, который теперь включает не только многообразие, но и все точки в пространстве вокруг него вплоть до максимального предела ошибки. Последний показан пунктирными красными окружностями на рис. А, а расширение набора данных — красными крестиками на рис. В. Автокодеру надо учиться сжимать все точки данных в этом пространстве до многообразия. Иными словами, обучаясь тому, какие аспекты точки данных обобщаемы и важны, а какие представляют собой «шум», шумопонижающий автокодер обучается аппроксимировать многообразие S .

Сформировав философскую мотивацию для шумопонижения, мы можем внести небольшие изменения в скрипт и создать шумопонижающий автокодер:

def corrupt_input(x):

corrupting_matrix = tf.random_uniform(shape=tf.shape(x) minval=0,maxval=2,dtype=tf.int32)

return x * tf.cast(corrupting_matrix, tf.float32)

x = tf.placeholder("float", [None, 784]) # mnist data image of

# shape 28*28=784

corrupt = tf.placeholder(tf.float32)

phase_train = tf.placeholder(tf.bool)

c_x = (corrupt_input(x) * corrupt) + (x * (1 — corrupt))

Этот фрагмент кода искажает входные данные, если заполнитель corrupt равен 1, и воздерживается от искажения, если он равен 0. Внеся это изменение, можно снова запустить автокодер и получить реконструкции, показанные на рис. 6.14. Очевидно, что шумопонижающий автокодер достоверно воспроизвел невероятную человеческую способность к дополнению недостающих фрагментов.

Рис. 6.14. Мы применяем операцию искажения к набору данных и обучаем шумопонижающий автокодер воссоздавать исходные, неискаженные изображения

Один из самых сложных аспектов глубокого обучения — проблема интерпретируемости . Это свойство модели машинного обучения, которое измеряет, насколько легко отслеживать и объяснять ее процессы и/или результаты. Интерпретировать глубокие модели обычно сложно из-за нелинейностей и большого числа параметров. Такие модели обычно точнее, но недостаточная интерпретируемость часто затрудняет их применение в очень важных, но рискованных областях. Например, если модель машинного обучения выдает, есть ли у пациента рак, врачу, вероятно, потребуется объяснение, чтобы подтвердить заключение.