Нихиль Будума - Основы глубокого обучения

from matplotlib import pyplot as plt

pca_recon = pca.inverse_transform(pca_codes[:1])

plt.imshow(pca_recon[0].reshape((28,28)), cmap=plt.cm.gray)

plt.show()

Этот фрагмент кода показывает, как визуализировать первое изображение в тестовом наборе данных, но легко модифицировать код, чтобы визуализировать любой произвольный их поднабор. Сравнение реконструкции метода главных компонент с реконструкциями автокодера на рис. 6.10 сразу дает понять, что автокодер значительно лучше PCA в работе с двумерными кодами. Результаты метода главных компонент хоть как-то приближены к результатам автокодера, который прошел только пять эпох обучения. У PCA большие проблемы с различением 5, 3 и 8, 0 и 8, 4 и 9. Повторение того же эксперимента с 30-мерными кодами дает значительное улучшение результатов PCA, но они все равно значительно хуже, чем результаты 30-мерного автокодера.

Рис. 6.10. Сравнение реконструкций метода главных компонент и автокодера

Чтобы завершить эксперимент, нужно загрузить сохраненную модель TensorFlow, получить двумерные коды и вывести коды как метода главных компонент, так и автокодера. Мы должны аккуратно перестроить граф TensorFlow именно так, как он выглядел во время обучения.

Мы задаем путь к контрольной точке модели, которую сохранили во время обучения как аргумент командной строки в скрипте. Наконец, используем собственную функцию, которая строит график с легендой и соответственно раскрашенными точками для данных разных классов цифр:

import tensorflow as tf

import autoencoder_mnist as ae

import argparse

def scatter(codes, labels):

colors = [

(‘#27ae60', ‘o'),

(‘#2980b9', ‘o'),

(‘#8e44ad', ‘o'),

(‘#f39c12', ‘o'),

(‘#c0392b', ‘o'),

(‘#27ae60', ‘x'),

(‘#2980b9', ‘x'),

(‘#8e44ad', ‘x'),

(‘#c0392b', ‘x'),

(‘#f39c12', ‘x'),

]

for num in xrange(10):

plt.scatter([codes[:,0][i] for i in xrange(len (labels)) if labels[i] == num],

[codes[:,1][i] for i in xrange(len(labels)) if labels[i] == num], 7,

label=str(num), color = colors[num][0], marker=colors[num][1])

plt.legend()

plt.show()

with tf.Graph(). as_default():

with tf.variable_scope("autoencoder_model"):

x = tf.placeholder("float", [None, 784])

phase_train = tf.placeholder(tf.bool)

code = ae.encoder(x, 2, phase_train)

output = ae.decoder(code, 2, phase_train)

cost, train_summary_op = ae.loss(output, x)

global_step = tf.Variable(0, name='global_step', trainable=False)

train_op = ae.training(cost, global_step)

eval_op, in_im_op, out_im_op, val_summary_op =

ae.evaluate(output, x)

saver = tf.train.Saver()

sess = tf.Session()

sess = tf.Session()

saver = tf.train.Saver()

saver.restore(sess, args.savepath[0])

ae_codes= sess.run(code, feed_dict={x:

mnist.test.images, phase_train: True})

scatter(ae_codes,

mnist.test.labels)

scatter(pca_codes, mnist.test.labels)

На визуализации (рис. 6.11) найти четкие кластеры для двумерных кодов метода главных компонент сложно, а автокодер прекрасно с этим справился, собрав вместе коды разных классов цифр.

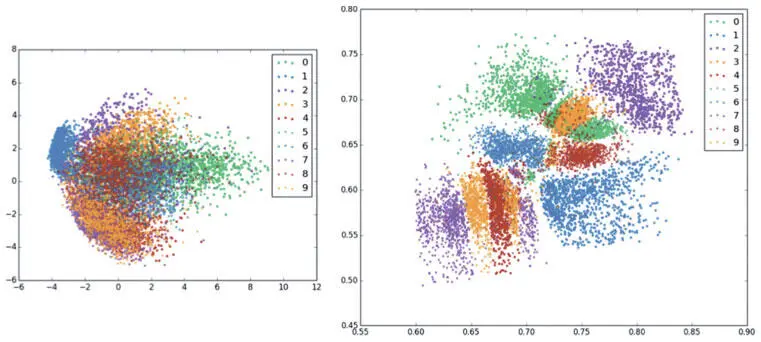
Рис. 6.11. Визуализируем двумерные представления метода главных компонент (слева) и автокодера (справа). Заметьте, что автокодер гораздо лучше группирует коды разных классов цифр

Простая модель машинного обучения способна классифицировать точки данных, состоящие из плотных представлений автокодера, гораздо эффективнее, чем из плотных представлений метода главных компонент.

Мы успешно создали и обучили автокодер с прямым распространением сигнала и показали, что полученные плотные векторные представления работают лучше, чем в методе главных компонент, классическом подходе к уменьшению размерности. В следующем разделе мы рассмотрим понятие шумопонижения, которое служит формой регуляризации, делая наши плотные векторные представления более эффективными.

Рассмотрим дополнительный механизм шумопонижения , повышающий способность автокодера порождать устойчивые к шуму плотные векторные представления. Человеческие органы восприятия удивительно устойчивы к шуму.

Возьмем, например, рис. 6.12. Хотя я исказил половину пикселов в каждом изображении, у вас едва ли возникли проблемы с распознаванием цифр. Даже те, которые легко перепутать (например, 2 и 7), вполне различимы.

Рис. 6.12. В верхнем ряду — исходные изображения из набора данных MNIST. В нижнем мы случайным образом затемнили половину пикселов. Однако человек способен различить цифры в этом ряду

Один из подходов к этому явлению — вероятностный. Даже если мы сталкиваемся со случайным удалением фрагментов изображения, при достаточном количестве информации мозг все равно обычно способен уяснить смысл. Он буквально заполняет пустоты и делает вывод.