Нихиль Будума - Основы глубокого обучения

При помощи TensorBoard можно визуализировать граф TensorFlow, ошибку на обучающем и проверочном наборах данных и информацию по изображениям. Выполните следующую команду:

$ tensorboard — logdir ~/path/to/mnist_autoencoder_hidden=2_logs

Затем наберите в браузере http://localhost:6006/ . Результаты из вкладки Graph показаны на рис. 6.6.

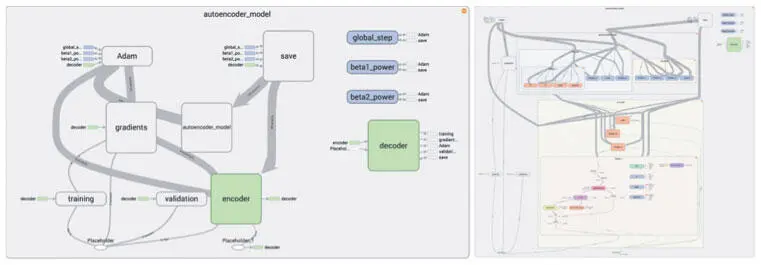
Рис. 6.6. TensorFlow позволяет в сжатом виде наблюдать основные компоненты и потоки данных нашего графа вычислений (слева), а также более подробно изучить потоки данных индивидуальных подкомпонентов (справа)

Мы удачно организовали пространство имен компонентов нашего графа TensorFlow, что способствовало хорошей организации всей модели. Можно легко переходить от одного компонента к другому и углубляться дальше, отслеживая движение данных по разным слоям кодера и декодера, чтение оптимизатором выходных данных модуля обучения и влияние градиентов на все компоненты модели.

Мы также визуализируем ошибку на обучающем (после каждого мини-пакета) и проверочном (после каждой эпохи) наборах данных, внимательно следя за кривыми, чтобы выявить возможное переобучение. Визуализации ошибки в TensorBoard приведены на рис. 6.7. Как и можно ожидать от успешной модели, и обучающий, и проверочный графики ошибки убывают, пока не выпрямляются асимптотически. После примерно 200 эпох мы добиваемся ошибки на проверочном множестве 4,78. Хотя кривые выглядят многообещающе, сложно сразу понять, достигли ли мы плато и величина ошибки «хорошая» или наша модель пока плохо воссоздает входные данные.

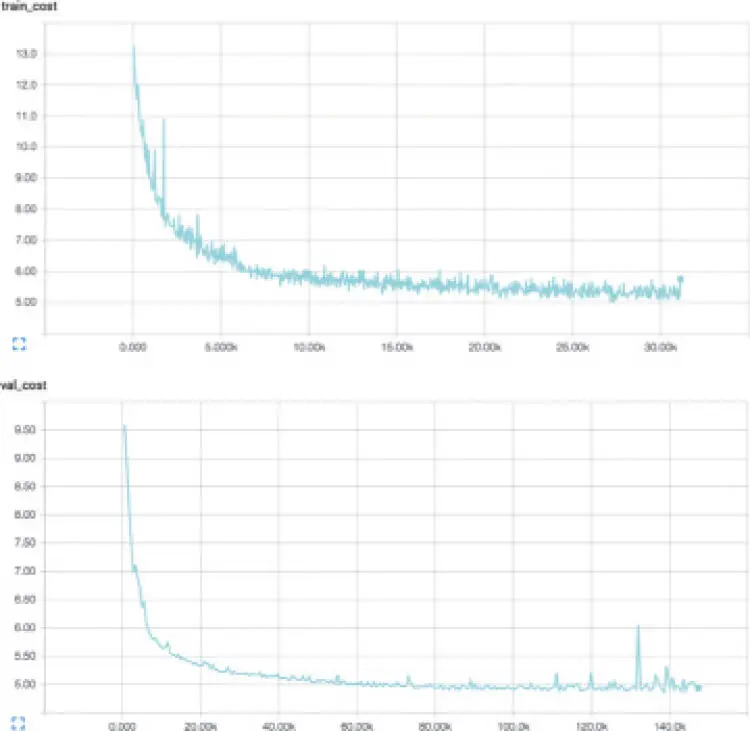
Рис. 6.7. Ошибка на обучающем (записаны после каждого мини-пакета) и проверочном наборах (записаны после каждой эпохи)

Чтобы понять, что это значит, рассмотрим набор данных MNIST. Возьмем произвольное изображение 1 из набора и назовем его X . На рис. 6.8 мы сравниваем его со всеми остальными в наборе. Для каждого класса цифр мы вычисляем среднее значение L2, сравнивая X с каждым примером класса цифр. Для визуализации включаем также среднее всех примеров каждого класса цифр.

Рис. 6.8. Изображение 1 слева сравнивается со всеми остальными цифрами в наборе данных MNIST; каждый класс цифр визуально представлен средним всех своих членов и помечен средним значением L2, единица слева сравнивается со всеми членами класса

X отстоит в среднем на 5,75 пункта от остальных единиц в MNIST. Если говорить о расстоянии L2, то ближайшие к Х цифры из не-единиц — семерки (8,94 пункта), а самые удаленные — нули (11,05 пункта). Эти показатели дают понять, что средняя ошибка автокодера 4,78 — высококачественная реконструкция.

Поскольку мы собираем результаты по изображениям, эту гипотезу можно подтвердить напрямую, рассмотрев сами входные изображения и их реконструкции. Реконструкции трех случайным образом выбранных образцов из тестового набора показаны на рис. 6.9.

Рис. 6.9. Сравнение входных данных из проверочного набора и их реконструкций после 5, 100 и 200 эпох обучения

После пяти эпох автокодер уже начинает улавливать примечательные черты исходного изображения, но по большей части реконструкции — туманный набор похожих цифр. После 100 эпох уверенно опознаются 0 и 4, но у автокодера остаются проблемы выбора между 5, 3 и, возможно, 8. После 200 эпох уже видно, что и эта неоднозначность устранена и все цифры распознаются четко.

Закончим раздел сравнением двумерных кодов, выданных традиционным методом главных компонент и автокодерами. Мы хотим показать, что автокодеры обеспечивают лучшую визуализацию, особенно разграничение разных классов цифр, чем метод главных компонент. Сначала быстро рассмотрим код, который используем для получения двумерных кодов методом главных компонент:

from sklearn import decomposition

import input_data

mnist = input_data.read_data_sets("data/", one_hot=False)

pca = decomposition.PCA(n_components=2)

pca.fit(mnist.train.images)

pca_codes = pca.transform(mnist.test.images)

Загрузим набор данных MNIST. Мы установили флаг one_hot=False, поскольку хотим, чтобы метки были представлены как целые числа, а не прямые унитарные векторы (напомним, что прямой унитарный вектор, отображающий метку MNIST, — вектор размера 10 с i -м компонентом, равным 1, для отображения цифры i , а остальные компоненты равны 0). Возьмем привычную библиотеку машинного обучения scikit-learn и выполним PCA, установив n_components=2, чтобы библиотека генерировала двумерные коды. Можно воссоздать исходные изображения из двумерных кодов и визуализировать реконструкции: