Нихиль Будума - Основы глубокого обучения

Сверточные архитектуры позволяют нам справиться с проклятием размерности, снижая число параметров в модели и не жертвуя выразительностью. Однако сверточным сетям все равно нужно много размеченных обучающих данных. И часто таких данных мало, а создавать их дорого. Наша цель в этой главе — разработать эффективные обучающиеся модели в таких ситуациях, когда размеченных данных мало, а «диких», неразмеченных очень много. Для этого мы будем обучать плотные векторные представления (embedding) , или представления с меньшей размерностью, без учителя. Поскольку модели без учителя позволяют выбирать признаки автоматически, мы можем при помощи сгенерированных плотных векторных представлений решать проблемы обучения для менее масштабных моделей, которым требуется меньше данных. Этот процесс представлен на рис. 6.1.

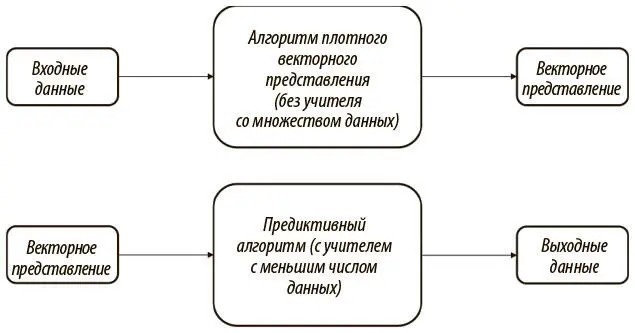
Рис. 6.1. Использование плотных векторных представлений позволяет автоматизировать выбор признаков при недостатке размеченных данных

В процессе разработки алгоритмов, хорошо обучающих плотные векторные представления, мы рассмотрим и другие варианты применения обучения представлений с меньшей размерностью — например, визуализацию и семантическое хэширование. Начнем с ситуаций, когда вся важная информация уже есть в самом входном векторе. В этом случае обучение плотного векторного представления эквивалентно разработке эффективного алгоритма сжатия.

В следующем разделе мы введем понятие метода главных компонент (PCA — principal component analysis), классического способа уменьшения размерности. Далее мы рассмотрим более эффективные нейронные методы обучения плотных представлений.

Основная идея метода главных компонент в том, что нам нужно найти такой набор осей, который будет передавать наибольшее количество информации о нашем наборе данных. А именно: если у нас есть d -размерные данные, нам нужно найти новый набор измерений m < d , который сохраняет максимально возможное количество ценной информации из исходного набора данных. Для удобства пусть d = 2, m = 1. Предположив, что вариативность связана с информацией, мы можем выполнить это преобразование с помощью итеративного процесса. Для начала находим единичный вектор, по которому набор данных наиболее вариативен. Поскольку это направление содержит больше всего информации, мы делаем его своей первой осью. Затем из набора векторов, ортогональных первому, мы выбираем новый единичный вектор, по которому набор данных опять же наиболее вариативен. Это вторая ось. Повторяем процесс, пока не находим d новых векторов, соответствующих новым осям. Проецируем наши данные на эти новые оси. Затем определяем подходящее значение m и избавляемся от всех осей, кроме m первых (главных компонент, которые содержат больше всего информации). Результат показан на рис. 6.2.

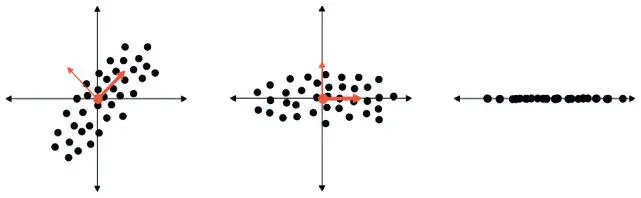
Рис. 6.2. Иллюстрация метода главных компонент для снижения размерности, сохраняющего измерение с наибольшим количеством информации (выраженном в вариативности)

Люди с математическим складом ума могут рассматривать эту операцию как проецирование на векторное пространство, порожденное верхними m собственными векторами ковариантной матрицы набора данных (при постоянном масштабе). Представим набор данных в виде матрицы Xс размерами n × d (то есть n входов и d измерений). Мы хотим создать вложенную матрицу Tс размерами n × m . Эту матрицу можно вычислить, используя отношения T = X, где каждый столбец Wсоответствует собственному вектору матрицы X Τ X.

Хотя метод главных компонент используется для снижения размерности уже несколько десятилетий, он почему-то не может сохранить важные отношения — как кусочно-линейные, так и кусочно-нелинейные. Возьмем пример, изображенный на рис. 6.3.

Рис. 6.3. Ситуация, в которой метод главных компонент не может оптимально преобразовать данные для снижения размерности

В этом примере показаны точки данных, случайно выбранные из двух концентрических кругов. Мы надеемся, что метод главных компонент преобразует этот набор данных так, чтобы мы смогли взять единую новую ось, которая позволит легко отделить красные точки от синих. К сожалению для нас, здесь нет такого линейного направления, которое содержит больше информации, чем любое другое (вариативность во всех направлениях равная). Мы, люди, отмечаем, что информация здесь кодируется нелинейно — тем, насколько точки удалены от центра. Имея в виду эту информацию, фиксируем, что преобразование к полярным координатам (выражение точек через их расстояние от центра в виде новой горизонтальной оси и через их угловое отклонение от первичной оси х в виде новой вертикальной оси) как раз справляется хорошо.