Нихиль Будума - Основы глубокого обучения

# apply dropout

fc_2_drop = tf.nn.dropout(fc_2, keep_prob)

with tf.variable_scope("output"):

output = layer(fc_2_drop, [192, 10], [10], phase_train)

return output

Наконец, при помощи оптимизатора Adam переходим к обучению сверточных сетей. Через какое-то время наши сети добиваются впечатляющей точности выполнения задачи по CIFAR-10: 92,3% без пакетной нормализации и 96,7% с ее использованием. Этот результат соответствует (а потенциально и превосходит) самому эффективному на данный момент варианту решении этой задачи! В следующем разделе мы подробнее рассмотрим визуализацию обучения и работы наших сетей.

Проще всего визуализировать обучение, построив функцию потерь на данных и проверки по мере прохождения процесса. Четко показать выгоды пакетной нормализации можно, сравнив скорости схождения двух наших сетей. Графики середины процесса тренировки приведены на рис. 5.17.

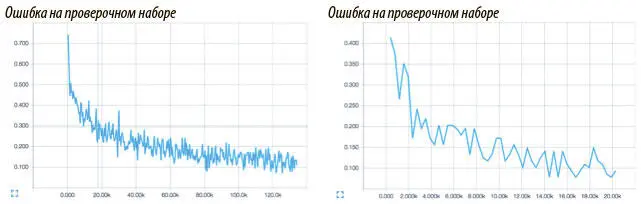
Рис. 5.17. Обучение сверточной сети без пакетной нормализации (слева) и с пакетной нормализацией (справа). Последняя значительно ускоряет процесс

Без пакетной нормализации достижение порога точности в 90% требует применения около 80 тысяч мини-пакетов. С пакетной же нормализацией этот порог достигается всего за 14 тысяч мини-пакетов.

Можно также рассмотреть фильтры, которым обучается наша сверточная сеть, и понять, что она считает важным для решений по классификации.

Сверточные слои обучаются иерархическим представлениям, и мы надеемся, что первый сверточный слой усвоит базовые признаки (края, простые кривые и т. д.), а второй — более сложные. К сожалению, интерпретация второго сверточного слоя сложна даже при визуализации, так что на рис. 5.18 представлены только фильтры первого слоя.

Рис. 5.18. Фрагмент набора выученных фильтров в первом сверточном слое нашей сети

У наших фильтров есть ряд интересных свойств: это вертикальные, горизонтальные и диагональные границы, а также небольшие точки или пятна одного цвета, окруженные другим. Безусловно, сеть обучается релевантным свойствам, поскольку фильтры точно нельзя считать обычным шумом.

Можно попытаться визуализировать то, как наша сеть научилась группировать разные виды изображений. Возьмем большую сеть, обученную на примере задач ImageNet, и рассмотрим скрытое состояние полносвязного слоя перед слоем подвыборки для каждого изображения.

Затем мы берем это многомерное представление каждого изображения и применяем алгоритм, известный как метод нелинейного снижения размерности и визуализации многомерных переменных ( t-Distributed Stochastic Neighbor Embedding , или t-SNE ), для сжатия до двумерного представления, которое уже можно визуализировать [68].

Подробно о t-SNE мы писать не будем, но есть много бесплатных доступных инструментов, в том числе код, которые нам помогут ( https://lvdmaaten.github.io/tsne/code/tsne_python.zip ). Мы визуализируем результаты на рис. 5.19, и они весьма впечатляющи.

Рис. 5.19. Визуализация представлений алгоритма t-SNE (в центре), окруженная увеличенными подсегментами представлений (по краям). © Андрей Карпати [69]

Сначала кажется, что изображения похожего цвета ближе друг к другу. Это интересно, но еще удивительнее другое: когда мы приближаем элементы визуализации, оказывается, что речь не только о цвете. Все изображения лодок находятся в одном месте, людей — в другом, а бабочек — в третьем сегменте визуализации. Очевидно, что возможности обучения сверточных сетей впечатляющи.

За последние пару лет мы разработали алгоритмы гораздо более сложного применения сверточных сетей. Один из них называется нейронным стилем [70]. Его цель — взять произвольную фотографию и переделать под стиль знаменитого художника. Задача кажется устрашающей, и не вполне понятно, как мы решили бы эту проблему, не будь сверточных сетей. Но оказывается, что умелое применение фильтров приводит к замечательным результатам.

Возьмем предварительно обученную сверточную сеть и три изображения. Первые два — источник содержания p (content) и источник стиля a (style). Третье — сгенерированное x . Наша задача — предложить функцию потерь для алгоритма обратного распространения ошибок так, чтобы при минимизации получилось идеальное сочетание содержания желаемой фотографии и стиля произведения искусства.