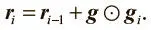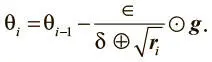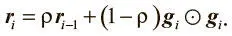Нихиль Будума - Основы глубокого обучения

Первым мы рассмотрим алгоритм AdaGrad, который стремится адаптировать общий темп обучения путем суммирования исторических градиентов. Впервые алгоритм был предложен в работе Джона Дучи и его коллег (2011) [50]. Мы сохраняем изменение темпа обучения для каждого параметра. Темп обратно масштабируется с учетом величины квадратного корня суммы квадратов (среднеквадратичного значения) всех исторических градиентов параметра. Можно выразить это математически. Мы инициализируем вектор суммирования градиента r 0 = 0. На каждом шаге мы суммируем квадраты градиентов всех параметров следующим образом (где операция — поэлементное умножение тензоров):

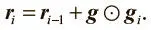
Затем мы обычным путем вычисляем обновление, но теперь глобальный темп обучения делится на квадратный корень вектора сумм градиента:

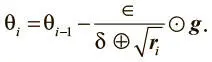
Заметьте, что мы добавляем в знаменателе небольшую величину δ (~10−7), чтобы избежать деления на 0. Кроме того, операции деления и сложения связаны с размером вектора суммирования градиента и применяются поэлементно. Встроенный в TensorFlow оптимизатор позволяет легко использовать AdaGrad в качестве алгоритма обучения:

tf.train.AdagradOptimizer(learning_rate,

initial_accumulator_value=0.1,

use_locking=False,

name='Adagrad')

Нужно только помнить, что в TensorFlow величина δ и исходный вектор суммирования градиента объединены в аргумент initial_accumulator_value.

На функциональном уровне такой механизм обновления означает, что параметры с наибольшими градиентами будут быстро снижать темп обучения, а с меньшими — незначительно. Можно констатировать, что AdaGrad обеспечивает больший прогресс на более пологих участках поверхности ошибок, помогая преодолеть плохо обусловленные поверхности. Теоретически это обеспечивает хорошие свойства, но на практике обучение глубоких моделей с помощью AdaGrad сопряжено с проблемами. По опыту можно сказать, что у него есть тенденция к преждевременному уменьшению темпа обучения, и он едва ли будет хорошо работать в некоторых глубоких моделях. Поговорим о RMSProp — алгоритме, призванном устранить этот недостаток.

AdaGrad хорошо работает с простыми выпуклыми функциями, но этот алгоритм не предназначен для сложных поверхностей ошибок глубоких сетей. Плоские области могут поставить AdaGrad в тупик, заставив снизить темп обучения еще до достижения минимума. Получается, простого сложения градиентов недостаточно.

Решением может стать идея, которую мы вводили при использовании импульса для снижения флуктуаций градиента. По сравнению с простым сложением экспоненциально взвешенные скользящие средние позволяют «отбрасывать» измерения, произведенные задолго до текущего момента. Обновление вектора суммирования градиента в этом случае выглядит так:

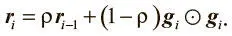
Коэффициент затухания ρ определяет, как долго мы будем хранить старые градиенты. Чем он ниже, тем меньше рабочее окно. Внеся такую модификацию в AdaGrad, мы получим алгоритм обучения RMSProp, впервые предложенный Джеффри Хинтоном [51].

В TensorFlow создать оптимизатор RMSProp можно с помощью следующего кода. Отметим, что в этом случае, в отличие от AdaGrad, мы вводим δ отдельно как эпсилон-аргумент конструктора:

tf.train.RMSPropOptimizer(learning_rate, decay=0.9,

momentum=0.0, epsilon=1e-10,

use_locking=False, name='RMSProp')

Как предполагает этот шаблон, можно использовать RMSProp в сочетании с импульсом (особенно нестеровским). В целом он показал себя эффективным средством оптимизации глубоких нейросетей и стал выбором по умолчанию для многих опытных практиков.

Прежде чем завершить разговор о современных средствах оптимизации, рассмотрим еще один алгоритм — Adam [52]. В принципе, можно считать его вариантом сочетания импульсного метода и RMSProp.

Основная идея такова. Мы хотим записывать экспоненциально взвешенное скользящее среднее градиента (скорость в классическом импульсном подходе), что можно выразить следующим образом:

m i = β 1 m i — 1 + (1 — β 1) g i.