Нихиль Будума - Основы глубокого обучения

Стоит воспользоваться этой информацией для разработки более эффективных алгоритмов оптимизации. Например, мы можем взять приближение второго порядка функции ошибок для определения скорости обучения на каждом этапе, больше всего снижающей функцию ошибки. Но оказывается, что точно вычислить матрицу Гессе — задача сложная. В следующих разделах мы рассмотрим открытия в оптимизации, которые позволяют справиться с плохой обусловленностью без непосредственного вычисления матрицы Гессе.

Проблема плохо обусловленной матрицы Гессе проявляется в серьезных флуктуациях градиентов. Один из популярных вариантов решения — отказ от вычисления гессиана и сосредоточение на борьбе с этими флуктуациями во время обучения. Один из способов понять, как такой подход может быть полезен, — изучить, как мяч катится по холмистой поверхности. Под действием силы тяжести он в итоге оказывается в низшей точке, но почему-то не страдает от серьезных флуктуаций и отклонений, которые случаются при градиентном спуске. В чем же дело? В отличие от стохастического градиентного спуска (при котором используется только градиент), движение мяча по поверхности ошибки определяется еще двумя основными компонентами. Первый, который мы моделируем в виде градиента при стохастическом спуске, в обиходе называется ускорением. Но не только оно определяет движение мяча. Гораздо важнее его скорость. Ускорение влияет именно на нее и лишь опосредованно — на положение мяча.

Движение под действием скорости желательно, поскольку оно противодействует значительным флуктуациям градиента, постепенно спрямляя траекторию мяча. Скорость — форма памяти, позволяющая эффективно аккумулировать движение к минимуму, сглаживая колебания ускорения в ортогональных направлениях. Наша задача — создать аналог скорости в алгоритме оптимизации. Это можно сделать, отслеживая экспоненциально взвешенное затухание предыдущих градиентов. Каждое обновление вычисляется с помощью сочетания обновления предыдущей итерации с текущим градиентом. Изменения вектора параметров определяются так:

v i = m v i − 1— ϵ g i ,

θ i = θ i − 1 + v i .

Иными словами, мы вводим гиперпараметр импульса m для определения того, какую долю предыдущей скорости нужно сохранить при обновлении, и добавляем «память» предыдущих градиентов к текущему. Этот метод обычно именуется импульсным . Поскольку введение импульса увеличивает размер шага, его использование порой требует сокращения скорости обучения по сравнению с обычным стохастическим градиентным спуском.

Чтобы нагляднее представить себе, как работает импульс, рассмотрим пример, как он влияет на обновления в ходе случайных блужданий , то есть совершения последовательности бессистемно выбранных шагов. Представим себе точку на линии, которая в каждый интервал времени случайно выбирает размер шага между –10 и 10 и перемещается в этом направлении. Это выражается просто:

step_range = 10

step_choices = range(-1 * step_range,step_range + 1)

rand_walk = [random.choice(step_choices) for x in xrange(100)]

Затем имитируем то, что произойдет при небольшой модификации импульса (с помощью стандартного алгоритма экспоненциально скользящего среднего), чтобы сгладить выбор шага на каждом интервале. Это можно кратко выразить так:

momentum_rand_walk = [random.choice(step_choices)]

for i in xrange(len(rand_walk) — 1):

prev = momentum_rand_walk[-1]

rand_choice = random.choice(step_choices)

new_step = momentum * prev + (1 — momentum) * rand_choice

momentum_rand_walk.append()

Результаты при варьировании импульса от 0 до 1 удивительны. Импульс существенно снижает волатильность обновлений. Чем он больше, тем мы менее чувствительны к новым обновлениям (например, серьезная неточность при первой оценке траектории сохраняется в течение значительного периода). Результаты эксперимента приведены на рис. 4.8.

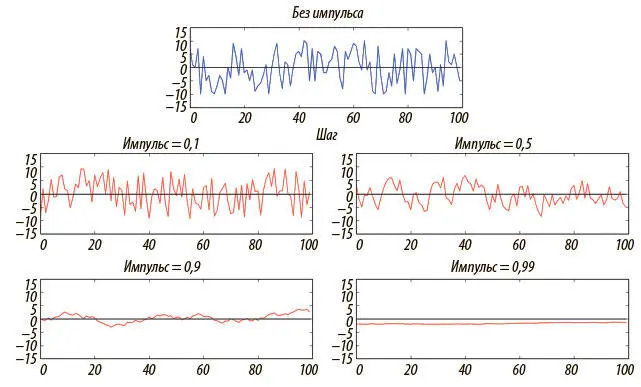
Рис. 4.8. Импульс снижает волатильность в размерах шагов при случайных блужданиях благодаря экспоненциально скользящему среднему

Чтобы понять, как импульс влияет на обучение реальных нейросетей с прямым распространением сигнала, мы можем вернуться к MNIST и применить импульсный оптимизатор TensorFlow. Будем использовать тот же темп обучения (0,01) с типичным импульсом 0,9:

learning_rate = 0.01

momentum = 0.9

optimizer = tf.train.MomentumOptimizer(learning_rate, momentum)

train_op = optimizer.minimize(cost, global_step=global_step)