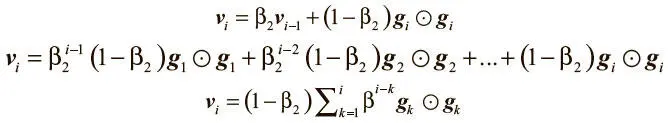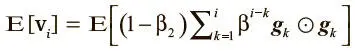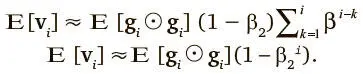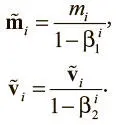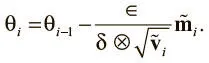Нихиль Будума - Основы глубокого обучения

Это аппроксимация так называемого первого импульса градиента, или E[ g i ]. Как и в RMSProp, можно сохранять экспоненциально взвешенное скользящее среднее исторических градиентов. Это оценка того, что называется вторым импульсом градиента, или E[ g i g i]:

v i = β 2 v i − 1 + (1 − β 2) g i g i .

Но оказывается, что эти приближения не соответствуют реальным импульсам, поскольку мы инициализируем оба вектора нулями. Чтобы устранить несоответствие, мы выводим поправочный коэффициент для обоих случаев. Здесь мы описываем вывод определения для второго импульса. Вывод первого импульса аналогичен, и мы оставим его в качестве упражнения для любителей математики.

Начнем с выражения определения второго импульса через все предыдущие градиенты. Для этого достаточно расширить рекуррентное соотношение:

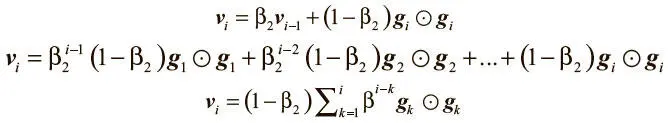
Возьмем ожидаемое значение обеих частей и определим, как наша оценка E[ v i ] соотносится с истинным значением E[ g i g i ]:

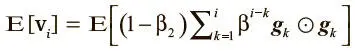
Можно принять, что E[ g k g k ] ≈E[ g i ≈ g i ], поскольку, даже если второй импульс градиента поменял значение по сравнению с историческим, β 2 должно быть выбрано так, чтобы прежние вторые импульсы градиентов утратили релевантность. В результате становится возможным такое упрощение:

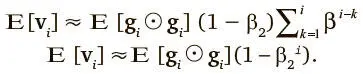
Последнее упрощение сделано с помощью элементарного алгебраического тождества 1 − x n = (1 − x ) (1 + x + … + x n — 1). В результате вывода второго импульса и аналогичного ему вывода первого мы получаем следующие поправочные схемы для борьбы с ошибкой инициализации:

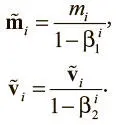
Теперь можно с помощью скорректированных импульсов обновить вектор параметров, что приведет к окончательному обновлению Adam:

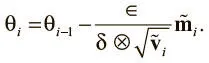
В последнее время Adam набрал популярность благодаря возможности исправлять ошибку нулевой инициализации (в RMSProp это слабое место) и способности эффективно сочетать ключевые идеи RMSProp и импульсного метода. В TensorFlow оптимизатор Adam создается с помощью следующего конструктора:

tf.train.AdamOptimizer(learning_rate=0.001, beta1=0.9,

beta2=0.999, epsilon=1e-08,

use_locking=False, name='Adam')

Настройки по умолчанию гиперпараметров для Adam в TensorFlow обычно работают удовлетворительно, но Adam хорошо справляется и с изменениями в них. Единственное исключение: иногда может понадобиться изменить темп обучения (по умолчанию задана величина 0,001).

В этой главе мы обсудили ряд стратегий для упрощения навигации по сложным поверхностям ошибок глубоких сетей. Они нашли свое высшее выражение в нескольких алгоритмах оптимизации, каждый из которых имеет свои достоинства и недостатки. Было бы замечательно заранее знать, когда какой алгоритм использовать, но практикующие эксперты пока не достигли здесь консенсуса. Сейчас самые популярные варианты — мини-пакетный градиентный спуск, мини-пакетный градиент в сочетании с импульсом, RMSProp, RMSProp в сочетании с импульсом, Adam и AdaDelta (об этом алгоритме мы здесь не говорили, а TensorFlow его пока не поддерживает). Мы включили в репозитории этой книги на Github скрипт TensorFlow, чтобы любознательный читатель мог поэкспериментировать с алгоритмами оптимизации на примере построенной модели сети с прямым распространением сигнала:

$ python optimzer_mlp.py

Важно отметить, однако, что для большинства практиков глубокого обучения лучший способ достичь вершин в своем деле состоит не в создании более совершенных оптимизаторов. Большинство прорывов в этой области за последние несколько десятилетий связаны с нахождением архитектур, которые проще обучать, а не попытками разобраться с неприятными поверхностями ошибок. Далее мы сосредоточимся на использовании архитектур для более эффективного обучения нейросетей.