Нихиль Будума - Основы глубокого обучения

Каждый из этих признаков сам по себе не особо эффективен при идентификации лица. Но при совместном использовании (в рамках классического алгоритма машинного обучения — бустинга, описанного в оригинальной работе ( http://bit.ly/2qMguNT )) их общая эффективность значительно возрастает. На наборе данных из 130 изображений и 507 лиц алгоритм достигает эффективности 91,4% при 50 ложных срабатываниях. Тогда такие показатели были беспрецедентными, но у этого алгоритма есть фундаментальные ограничения. Если лицо частично затенено, сравнение интенсивности света не срабатывает. Более того, если алгоритм «смотрит» на морщинистое лицо или лицо персонажа мультфильма, неудача почти неизбежна.

Алгоритм на самом деле так и не научился «смотреть». Помимо различий в интенсивности света, наш мозг использует обширный спектр визуальных подсказок для определения того, что мы видим человеческое лицо. Это контуры, относительное расположение черт и цвет. И даже если одна из визуальных подсказок содержит расхождения (например, части лица скрыты или затенены), зрительная кора все равно с высокой надежностью способна вычленять лица.

Чтобы с помощью традиционных методов научить компьютер «видеть», нужно дать программе гораздо больше признаков. Только так можно добиться более точных решений. До эры глубокого обучения огромные коллективы исследователей компьютерного зрения многие годы спорили о пользе разных признаков. Поскольку задачи распознавания становились всё сложнее, ученым часто приходилось тяжело.

Чтобы проиллюстрировать возможности глубокого обучения, рассмотрим соревнование ImageNet — одно из самых престижных в области компьютерного зрения (иногда его даже называют Олимпийскими играми компьютерного зрения) [57]. Каждый год исследователи пытаются разбить изображения по 200 возможным классам на основе обучающего набора данных примерно из 450 тысяч образцов. Алгоритму дается пять попыток на ответ, прежде чем он переходит к следующему изображению из тестового набора. Цель — довести компьютерное зрение до уровня человеческого (примерно 95–96% точности). В 2011 году победитель соревнования ImageNet показал частоту ошибок 25,7%, в среднем одно изображение из четырех [58]. Конечно, это большой шаг по сравнению с гаданием, но для коммерческого применения такой результат не подходит.

В 2012 году Алекс Крижевский из лаборатории Джеффри Хинтона в Университете Торонто совершил невозможное. Он впервые применил архитектуру глубокого обучения, ныне известную как сверточная нейросеть , к проблемам особого масштаба и сложности, не оставив соперникам шансов. Второе место занял участник с похвальным результатом 26,1%. А вот AlexNet всего за несколько месяцев работы побила все рекорды 50-летних исследований в области традиционного компьютерного зрения с частотой появления ошибок примерно 16% [59]. Не будет преувеличением сказать, что она единолично ввела глубокое обучение в работу над компьютерным зрением. Произошла настоящая революция в этой области.

Фундаментальная цель применения глубокого обучения к компьютерному зрению — отказ от трудоемкого и имеющего значительные ограничения процесса выбора признаков. Как мы уже говорили в главе 1, глубокие нейросети идеальны для такого процесса, поскольку каждый их слой отвечает за усвоение и создание признаков, представляющих получаемые входные данные. Наивный подход мог бы состоять в использовании обычной глубокой нейросети вроде той, что мы разработали в главе 3, и применении ее к набору данных MNIST для решения проблемы классификации изображений. Но при таком методе мы вскоре столкнемся с очень неприятными трудностями, которые показаны на рис. 5.3.

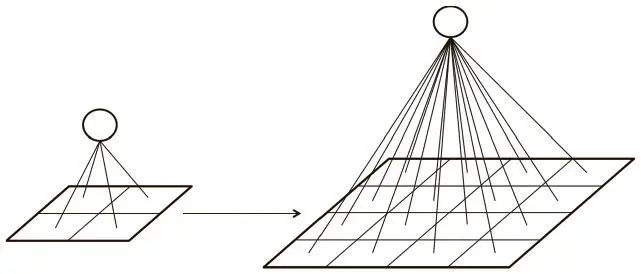
Рис. 5.3. Плотность связей между слоями неприемлемо возрастает с увеличением размера изображения

В MNIST наши изображения имели масштаб всего 28×28 пикселов и к тому же были черно-белыми. В результате у нейрона в полносвязном скрытом слое было всего 784 входящих веса. Это нормально для работы с MNIST, и наша обычная нейросеть функционировала хорошо. Однако этот метод не масштабируется на более объемные изображения. Например, для полноцветного изображения 200×200 пикселов входной слой будет иметь 200×200×3 = 120 000 весов. А нам нужно будет разместить множество нейронов по разным слоям, и число параметров будет расти очень быстро! Полная связность не только окажется излишней, но и обусловит значительно большие шансы на переобучение.