Обозначим k -ю карту признаков в слое m как m k . Далее обозначим соответствующий фильтр по значениям его весов W . Предположим, что у нейронов на карте признаков может быть смещение b k (оно идентично для всех нейронов на карте признаков), и теперь мы можем математически выразить карту признаков:
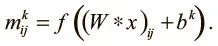
Это математическое выражение, конечно, простое и сжатое, но не до конца описывает применение фильтров в сверточных нейронных сетях. Те работают не только на одной карте признаков. Они действуют по всему объему карт, созданных на конкретном слое. Рассмотрим, например, ситуацию, когда нам нужно определить лицо на конкретном уровне сверточной сети. Мы аккумулируем три карты признаков: одну для глаз, одну для носов, одну для ртов. Мы знаем, что на определенном участке изображения есть лицо, если соответствующие участки на базовых картах содержат подходящие признаки (два глаза, нос и рот). Иными словами, чтобы определить наличие лица на изображении, мы должны свести воедино свидетельства нескольких карт. Это столь же необходимо и для полноцветного изображения. Пикселы в нем представлены в виде значений шкалы RGB, и во входном объеме нам потребуется три сектора (по одному для каждого цвета). Итак, карты признаков должны уметь работать на объемах, а не только плоскостях. Это показано на рис. 5.8. Каждая клетка входного объема — нейрон. Локальная область умножается на фильтр (соответствующий весам в сверточном слое), и образуется нейрон на карте фильтров в объемном слое нейронов.
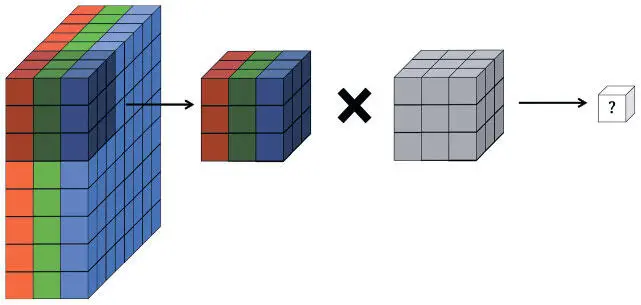
Рис. 5.8. Представление полноцветного RGB-изображения в виде объема и наложение объемного сверточного фильтра
Как мы уже говорили в предыдущем разделе, сверточный слой (состоящий из набора фильтров) преобразует один набор значений в другой. Глубина фильтра соответствует глубине входного объема. Фильтр может комбинировать информацию обо всех выученных признаках. Глубина исходящего объема сверточного слоя эквивалентна числу фильтров в нем, ведь каждый фильтр порождает свой сектор. Эти отношения показаны на рис. 5.9.
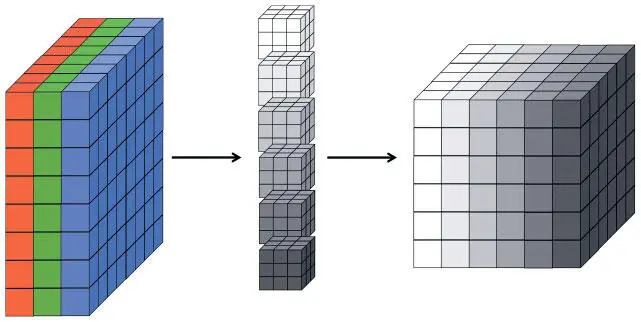
Рис. 5.9. Трехмерная визуализация сверточного слоя, где каждый фильтр соответствует сектору в получившемся выходном объеме
В следующем разделе мы применим эти концепции и заполним ряд пробелов, чтобы дать полное описание сверточного слоя.
Полное описание сверточного слоя
Воспользуемся выведенными понятиями и завершим описание сверточного слоя. Во-первых, он принимает следующие входящие характеристики.
• Ширина w in .
• Высота h in .
• Глубина d in .
• Дополнение нулями p .
Входные значения обрабатываются фильтрами в количестве k , которые соответствуют весам и связям в сверточной сети. У фильтров есть ряд гиперпараметров, которые описываются так:
• Пространственная протяженность e , равная высоте и ширине фильтра.
• Сдвиг s , или дистанция между последовательными применениями фильтра к объему входных данных. Если использовать сдвиг 1, получится полная свертка, описанная в предыдущем разделе. Проиллюстрируем это на рис. 5.10.
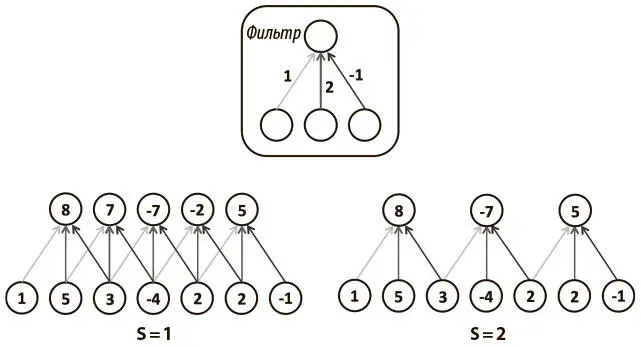
Рис. 5.10. Иллюстрация гиперпараметра сдвига фильтра
• Смещение b (параметр, определяемый в процессе обучения, как и значения фильтра), добавляемый к каждому компоненту свертки.
Получаем выходные данные со следующими характеристиками.
• Функция активации f , применяемая ко входному логиту каждого нейрона в объеме входных данных для определения выходного значения.
• Ширина 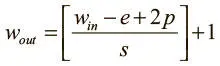 .
.
• Высота 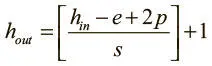 .
.
• Глубина d out = k .
m -й «срез по глубине» объема выходных значений, где 1 ≤ m ≤ k , соответствует функции активации f , примененной к сумме m -го фильтра, свернутого по объему входящих значений и смещения b m . Более того, это значит, что на фильтр мы имеем d ine 2параметров. Всего в слое kd ine 2параметров и k смещений.
Читать дальше
Конец ознакомительного отрывка
Купить книгу

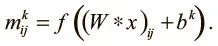



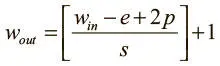 .
.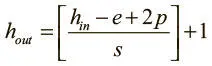 .
.










