Чтобы продемонстрировать это в действии, мы приводим пример сверточного слоя на рис. 5.11 и 5.12 с объемом входных значений 5×5×3 и дополнением нулями p = 1. Возьмем два фильтра 3×3×3 (пространственная протяженность) со сдвигом s = 2. Мы применим линейную функцию и получим объем выходных данных размером 3×3×2.
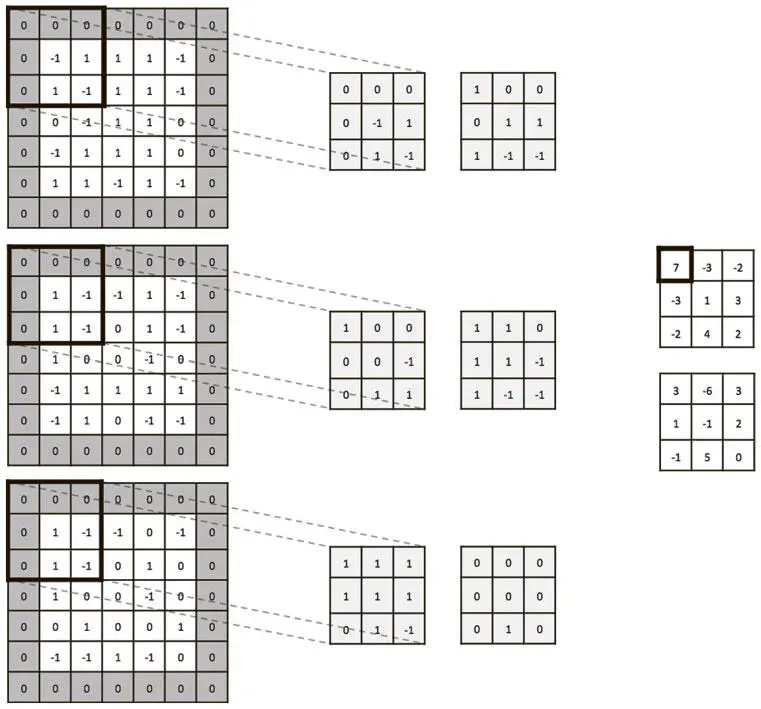
Рис. 5.11. Сверточный слой с объемом входных значений шириной 5, высотой 5, глубиной 3 и дополнением нулями 1. Есть два фильтра пространственной протяженностью 3, применяемые со сдвигом 2. Получается объем выходных данных шириной 3, высотой 3 и глубиной 2. Первый сверточный фильтр мы применяем к верхнему левому сегменту объема входных данных 3×3 и получаем верхний левый элемент среза по глубине
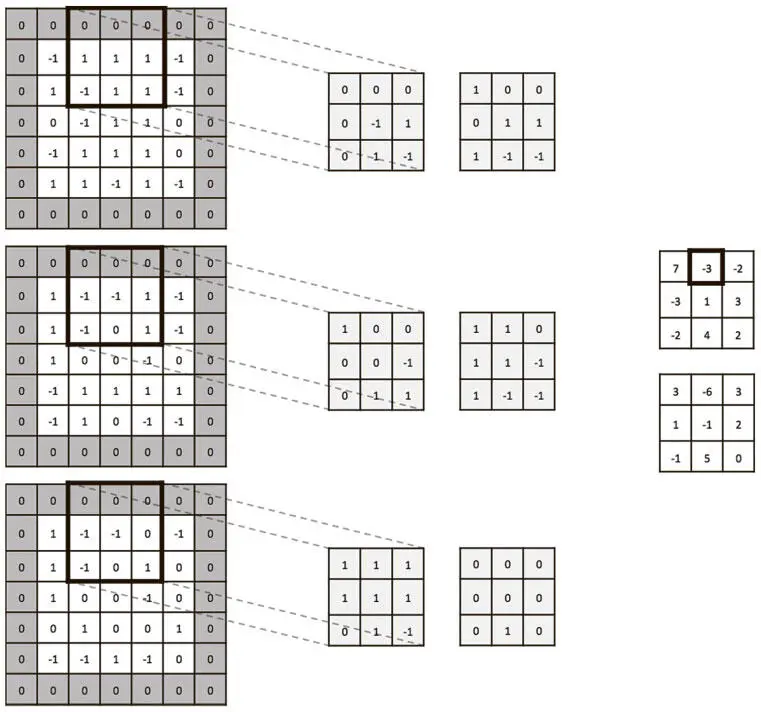
Рис. 5.12. Так же, как на рис. 5.11, мы порождаем следующее значение в первом срезе по глубине объема выходных данных
Разумно использовать фильтры небольших размеров (3×3 или 5×5). Реже применяются более крупные размеры (7×7), и то для первого сверточного слоя. Множество мелких фильтров повышает результативность и позволяет ограничиться меньшим числом параметров. Также предлагаем пользоваться сдвигом 1, чтобы ничего не упустить на карте признаков, и дополнение нулями, которое помогает достичь эквивалентности высоты и ширины объема входных и входных данных.
TensorFlow позволяет совершать удобные операции, легко сворачивая мини-пакет объемов входных данных (функцию активации f мы должны выбрать самостоятельно — операция не применит ее сама) [62]:
tf.nn.conv2d(input, filter, strides, padding,
use_cudnn_on_gpu=True, name=None)
Здесь input — четырехмерный тензор размера N × h in × w in × d in , где N — количество примеров в мини-пакете. Аргумент filter — тоже четырехмерный тензор, представляющий все фильтры, которые применены при свертке. Он имеет размер e × e × d in × k . Полученный при этой операции тензор имеет ту же структуру, что и input. Задав в padding значение SAME, мы выбираем дополнение нулями, так что высота и ширина сохраняются сверточным слоем.
Max Pooling (операция подвыборки)
Чтобы резко уменьшить размерность карт признаков и заострить внимание на найденных признаках, мы иногда используем слой max pooling (слой операции подвыборки) после сверточного [63]. Смысл его — в разбиении карты на сектора равного размера. Так мы получаем сжатую карту признаков. Фактически мы создаем свою ячейку для каждого сектора, вычисляем максимальное значение по нему и записываем его в соответствующую ячейку сжатой карты признаков. Этот процесс показан на рис. 5.13.
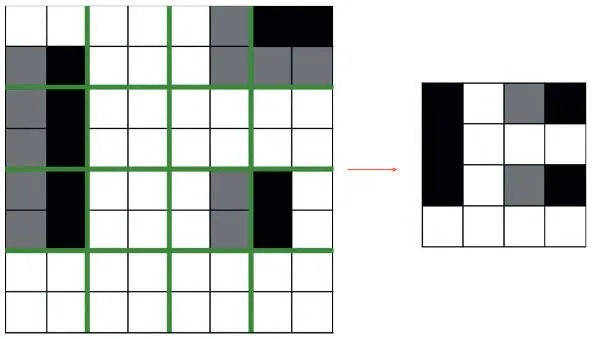
Рис. 5.13. Иллюстрация того, как max pooling значительно сокращает параметры при продвижении по сети
Более строго слой подвыборки можно описать при помощи двух параметров:
• пространственной протяженности e ;
• сдвига s .
Важно отметить, что используются лишь два основных варианта слоя подвыборки. Первый — неперекрывающийся с параметрами e = 2, s = 2. Второй — перекрывающийся с e = 3, s = 2. Получаем следующие размеры каждой карты признаков.
• Ширина 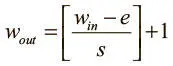 .
.
• Высота 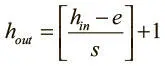 .
.
Интересное свойство max pooling — локальная инвариантность . Даже если входные значения немного варьируются, выходные остаются неизменными. Это имеет важные последствия для визуальных алгоритмов. Локальная инвариантность — очень полезное свойство, если нас больше интересует то, есть ли вообще данный признак, а не то, где именно он находится. Но в больших объемах она может повредить способности нашей сети переносить важную информацию. Поэтому пространственная протяженность слоев подвыборки должна оставаться небольшой.
В недавних исследованиях Бенджамин Грэм из Университета Уорвика [64]предложил идею дробного max pooling . При этом подходе используется генератор псевдослучайных чисел: он создает разбиение на области нецелой длины для дальнейшей подвыборки. Дробное max pooling работает сильным регуляризатором, помогая предотвратить переобучение сверточных нейросетей.
Читать дальше
Конец ознакомительного отрывка
Купить книгу




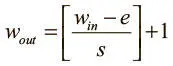 .
.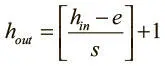 .
.










