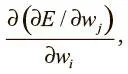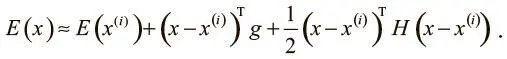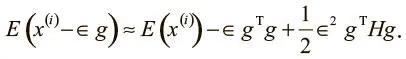Что все это значит в контексте оптимизации моделей глубокого обучения? Для стохастического градиентного спуска — пока непонятно. Судя по всему, плоские области на поверхности ошибок неприятны, но не мешают получить приемлемый ответ с использованием этого метода. Но они создают серьезные проблемы для методов, которые пытаются найти прямое решение в точке, где градиент равен 0. Именно это обстоятельство снижает пользу некоторых методов оптимизации второго порядка для моделей глубокого обучения, о чем мы поговорим ниже.
Когда градиент указывает в неверном направлении
При анализе поверхностей ошибок глубоких сетей, судя по всему, самое важное в оптимизации — поиск верной траектории. Неудивительно, что чаще всего эта проблема встает при рассмотрении поверхности ошибок вокруг локального минимума. В качестве примера рассмотрим поверхность ошибки, определенную двумерной областью параметров, на рис. 4.6.
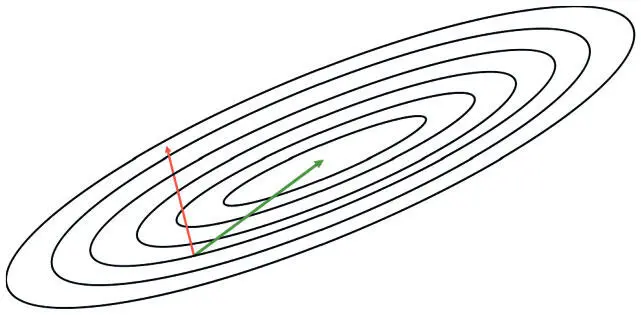
Рис. 4.6. Локальная информация, представленная градиентом, обычно не соответствует глобальной структуре поверхности ошибок
Вновь обратившись к контурным диаграммам, о которых шла речь в главе 2, мы отмечаем, что градиент — обычно не лучший индикатор правильной траектории. Он указывает в направлении локального минимума, только если контуры идеально круглые. Если же они эллиптические (как обычно и бывает с поверхностями ошибок глубоких сетей), градиент может указывать на 90° в сторону от верного направления!
Распространим этот анализ на произвольное число измерений, введя несколько математических обозначений. Для каждого веса w i в области параметров градиент вычисляет значение 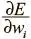 , или то, как меняется значение ошибки при вариациях значения w i . Определив и объединив все веса в области параметров, градиент дает направление кратчайшего спуска. Однако, прежде чем сделать уверенный шаг в этом направлении, нужно вспомнить о проблеме: градиент может меняться у нас на глазах в процессе движения! Этот простой факт показан на рис. 4.7. Возвращаясь к двумерному примеру, скажем: если наши контуры идеально круглые и мы делаем значительный шаг в направлении наискорейшего спуска, градиент больше направления не меняет. Но для сильно эллиптических контуров это неверно.
, или то, как меняется значение ошибки при вариациях значения w i . Определив и объединив все веса в области параметров, градиент дает направление кратчайшего спуска. Однако, прежде чем сделать уверенный шаг в этом направлении, нужно вспомнить о проблеме: градиент может меняться у нас на глазах в процессе движения! Этот простой факт показан на рис. 4.7. Возвращаясь к двумерному примеру, скажем: если наши контуры идеально круглые и мы делаем значительный шаг в направлении наискорейшего спуска, градиент больше направления не меняет. Но для сильно эллиптических контуров это неверно.

Рис. 4.7. Мы показываем, как направление градиента меняется, когда мы следуем в направлении скорейшего спуска (определенного от начальной точки). Векторы нормализованы до идентичной длины, чтобы подчеркнуть смену их направления
В общем случае мы можем определить изменения градиента во время спуска в определенном направлении, вычислив вторую производную. Мы подсчитываем
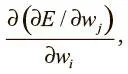
что дает возможность определить, как градиентный компонент w j модифицируется с изменением значения w i . Эту информацию мы можем свести в особую матрицу, известную как матрица Гессе, или гессиан ( Н ). При описании поверхности ошибок, когда градиент меняется в ходе пути в направлении кратчайшего спуска, она называется плохо обусловленной .
Для математически подкованных читателей подробнее расскажем о том, как гессиан ограничивает оптимизацию только с помощью градиентного спуска. Определенные свойства матрицы Гессе (реальность и симметричность) позволяют успешно определить вторую производную (которая аппроксимирует кривизну поверхности) при движении в определенном направлении. А именно: если есть единичный вектор d , вторая производная в этом направлении задается d Hd . Теперь можно использовать аппроксимацию второго порядка с помощью ряда Тейлора и понять, что происходит с функцией ошибок при переходе от текущего вектора параметров x (i)к новому xпо вектору градиента g [44], выраженному в x (i) :
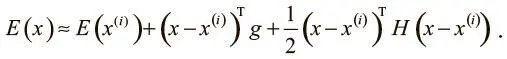
Если мы будем и далее двигаться в направлении градиента, можно упростить наше выражение:
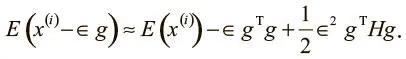
Оно состоит из трех членов: 1) значение функции потерь для исходного вектора параметров; 2) улучшение функции потерь, обеспеченное величиной градиента; 3) корректирующий член, который выражает кривизну пространства, представленную матрицей Гессе.
Читать дальше
Конец ознакомительного отрывка
Купить книгу


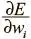 , или то, как меняется значение ошибки при вариациях значения w i . Определив и объединив все веса в области параметров, градиент дает направление кратчайшего спуска. Однако, прежде чем сделать уверенный шаг в этом направлении, нужно вспомнить о проблеме: градиент может меняться у нас на глазах в процессе движения! Этот простой факт показан на рис. 4.7. Возвращаясь к двумерному примеру, скажем: если наши контуры идеально круглые и мы делаем значительный шаг в направлении наискорейшего спуска, градиент больше направления не меняет. Но для сильно эллиптических контуров это неверно.
, или то, как меняется значение ошибки при вариациях значения w i . Определив и объединив все веса в области параметров, градиент дает направление кратчайшего спуска. Однако, прежде чем сделать уверенный шаг в этом направлении, нужно вспомнить о проблеме: градиент может меняться у нас на глазах в процессе движения! Этот простой факт показан на рис. 4.7. Возвращаясь к двумерному примеру, скажем: если наши контуры идеально круглые и мы делаем значительный шаг в направлении наискорейшего спуска, градиент больше направления не меняет. Но для сильно эллиптических контуров это неверно.