h2_W_inter = var_list_opt[2] * beta + var_list_rand[2] * alpha
h2_b_inter = var_list_opt[3] * beta + var_list_rand[3] * alpha
o_W_inter = var_list_opt[4] * beta + var_list_rand[4] * alpha
o_b_inter = var_list_opt[5] * beta + var_list_rand[5] * alpha
h1_inter = tf.nn.relu(tf.matmul(x, h1_W_inter) + h1_b_inter)
h2_inter = tf.nn.relu(tf.matmul(h1_inter, h2_W_inter) + h2_b_inter)
o_inter = tf.nn.relu(tf.matmul(h2_inter, o_W_inter) + o_b_inter)
cost_inter = loss(o_inter, y)
Наконец, мы можем варьировать значение alpha, чтобы определить, как меняется поверхность ошибок при переходе вдоль линии от случайным образом инициализированной точки к конечному решению стохастическим градиентным спуском:
import matplotlib.pyplot as plt
summary_writer = tf.train.SummaryWriter("linear_interp_logs/", graph_def=sess.graph_def)
summary_op = tf.merge_all_summaries()
results = []
for a in np.arange(-2, 2, 0.01):
feed_dict = {
x: mnist.test.images,
y: mnist.test.labels,
alpha: [[a]],
}
cost, summary_str = sess.run([cost_inter, summary_op], feed_dict=feed_dict)
summary_writer.add_summary(summary_str, (a + 2)/0.01)
results.append(cost)
plt.plot(np.arange(-2, 2, 0.01), results, ‘ro')
plt.ylabel(‘Incurred Error')
plt.xlabel(‘Alpha')
plt.show()
Получаем рис. 4.3, который мы можем проанализировать сами. Если мы будем повторять этот эксперимент, окажется, что никаких локальных минимумов, которые всерьез поставили бы нас в тупик, и нет. Судя по всему, основная сложность с градиентным спуском — не они, а трудности с выбором нужного направления. К этому вопросу мы вернемся чуть позже.
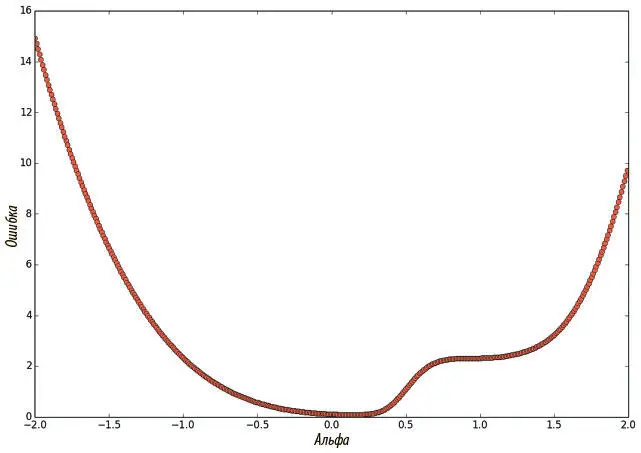
Рис. 4.3. Функция потерь трехслойной нейросети с прямым распространением сигнала при линейной интерполяции на линию, соединяющую случайным образом инициализированный вектор параметров и решение стохастического градиентного спуска
Плоские области на поверхности ошибок
Хотя наш анализ и показал отсутствие проблем с локальными минимумами, можно отметить особенно плоскую область, в которой градиент доходит до нуля, а alpha = 1. Это не локальный минимум, и вряд ли она поставит нас в затруднение, но кажется, что нулевой градиент может замедлить обучение.
В общем случае для произвольной функции точка, на которой градиент становится нулевым вектором, называется критической . Критические точки бывают разных типов. Мы уже говорили о локальных минимумах, несложно представить себе и их противоположности: локальные максимумы , которые, впрочем, не вызывают особых проблем при стохастическом градиентном спуске. Но есть и странные точки, лежащие где-то посередине. Эти «плоские» области — потенциально неприятные, но не обязательно смертельные — называются седловыми точками . Оказывается, когда у нашей функции появляется все больше измерений (а у модели все больше параметров), седловые точки становятся экспоненциально более вероятными, чем локальные минимумы. Попробуем понять, почему так происходит.
Для одномерной функции ошибок критическая точка может принимать одну из трех форм, как показано на рис. 3.1. Представим себе, например, что все эти три конфигурации одинаково вероятны. Если взять случайную критическую точку случайной одномерной функции, то вероятность того, что это локальный минимум, будет равна 1/3. И если у нас есть k критических точек, то можно ожидать, что локальными минимумами окажутся k/ 3 из них.
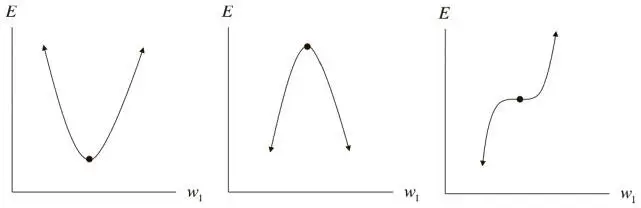
Рис. 4.4. Анализ критической точки в одном измерении
Можно распространить это утверждение на функции с большим числом измерений. Представим функцию потерь в d -мерном пространстве. Возьмем произвольную критическую точку. Оказывается, определить, будет ли она локальным минимумом, локальным максимумом или седловой точкой, сложнее, чем для одномерного случая. Рассмотрим поверхность ошибок на рис. 4.5. В зависимости от того, как выбирать направление (от A к B или от C к D), критическая точка будет казаться либо минимумом, либо максимумом. В реальности она ни то ни другое. Это более сложный тип седловой точки.
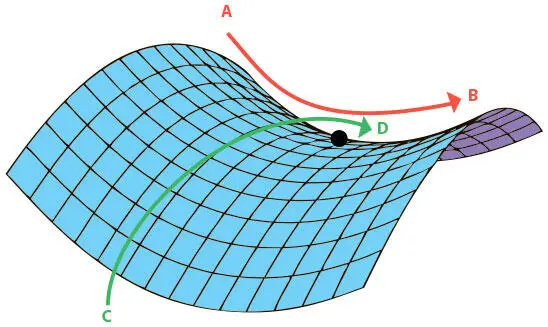
Рис. 4.5. Седловая точка на двумерной поверхности ошибок
В целом в d -мерной области параметров мы можем провести через критическую точку d различные оси. Она может быть локальным минимумом, только если оказывается локальным минимумом в каждой из d одномерных подобластей. Зная, что критическая точка в одномерной подобласти может относиться к одному из трех типов, мы понимаем: вероятность того, что случайная критическая точка принадлежит случайной функции, равна 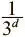 . Это значит, что случайная функция с k критических точек имеет ожидаемое количество
. Это значит, что случайная функция с k критических точек имеет ожидаемое количество 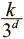 локальных минимумов. С ростом размерности области параметров число локальных минимумов экспоненциально уменьшается. Более строгое рассмотрение этой темы выходит за рамки настоящей книги; ознакомиться с вопросом можно в работе Яна Дофина и его коллег (2014) [43].
локальных минимумов. С ростом размерности области параметров число локальных минимумов экспоненциально уменьшается. Более строгое рассмотрение этой темы выходит за рамки настоящей книги; ознакомиться с вопросом можно в работе Яна Дофина и его коллег (2014) [43].
Читать дальше
Конец ознакомительного отрывка
Купить книгу




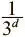 . Это значит, что случайная функция с k критических точек имеет ожидаемое количество
. Это значит, что случайная функция с k критических точек имеет ожидаемое количество 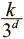 локальных минимумов. С ростом размерности области параметров число локальных минимумов экспоненциально уменьшается. Более строгое рассмотрение этой темы выходит за рамки настоящей книги; ознакомиться с вопросом можно в работе Яна Дофина и его коллег (2014) [43].
локальных минимумов. С ростом размерности области параметров число локальных минимумов экспоненциально уменьшается. Более строгое рассмотрение этой темы выходит за рамки настоящей книги; ознакомиться с вопросом можно в работе Яна Дофина и его коллег (2014) [43].










