Нихиль Будума - Основы глубокого обучения

Используя модель логистической регрессии, мы сократили частоту ошибок в наборе данных MNIST до 8,1%. Показатель впечатляющий, но для практического применения он не особо подходит.

Например, если система используется для проверки чеков на четырехзначные суммы (от 1000 до 9999 долларов), ошибки будут допускаться почти в 30% случаев! Чтобы создать более точную программу для чтения цифр из MNIST, построим нейросеть с прямым распространением сигнала.

Мы создаем такую модель с двумя скрытыми слоями, каждый из которых состоит из 256 нейронов ReLU (рис. 3.7).

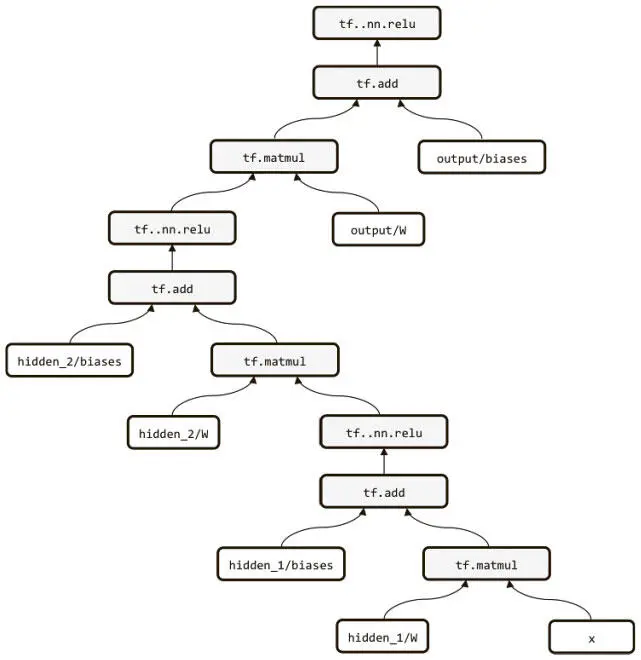
Рис. 3.7. Сеть с прямым распространением сигнала на нейронах ReLU с двумя скрытыми слоями

Мы можем использовать б о льшую часть кода из примера для логистической регрессии, внеся всего несколько изменений:

def layer(input, weight_shape, bias_shape):

weight_stddev = (2.0/weight_shape[0])**0.5

w_init = tf.random_normal_initializer(stddev=weight_stddev)

bias_init = tf.constant_initializer(value=0)

W = tf.get_variable("W", weight_shape, initializer=w_init)

b = tf.get_variable("b", bias_shape, initializer=bias_init)

return tf.nn.relu(tf.matmul(input, W) + b)

def inference(x):

with tf.variable_scope("hidden_1"):

hidden_1 = layer(x, [784, 256], [256])

with tf.variable_scope("hidden_2"):

hidden_2 = layer(hidden_1, [256, 256], [256])

with tf.variable_scope("output"):

output = layer(hidden_2, [256, 10], [10])

return output

Новый код по большей части говорит сам за себя, но стратегия инициализации заслуживает дополнительного описания. Качество работы глубоких нейросетей во многом зависит от эффективности инициализации их параметров. Как мы расскажем в следующей главе, у поверхностей ошибок таких сетей много свойств, значительно усложняющих оптимизацию с помощью стохастического градиентного спуска.

Проблема усугубляется при росте числа слоев в модели, а следовательно, и сложности поверхности ошибок. Один из способов ее устранения — умная инициализация. Исследование 2015 года, опубликованное К. Хе и его коллегами, показывает, что для нейронов ReLU дисперсия весов в сети должна быть равна 2/ n in, где n in — число входов в нейрон [40]. Любопытному читателю стоит рассмотреть, что произойдет при изменении инициализации. Например, если снова заменить tf.random_normal_initializer на tf.random_uniform_initializer, который мы использовали в примере с логистической регрессией, результаты серьезно ухудшатся.

Наконец, чтобы еще немного улучшить качество работы, мы вычисляем функцию мягкого максимума при вычислении ошибки, а не на стадии предсказания. Отсюда новая модификация:

def loss(output, y):

xentropy = tf.nn.softmax_cross_entropy_with_logits(output, y)

loss = tf.reduce_mean(xentropy)

return loss

Работа программы на протяжении 300 эпох выдает значительные улучшения по сравнению с моделью логистической регрессии. Она функционирует с аккуратностью 98,2%, почти на 78% снижая частоту ошибок на знак по сравнению с первым вариантом.

В этой главе мы больше узнали о том, как использовать TensorFlow в качестве библиотеки для представления и обучения наших моделей. Мы поговорили о ряде ее важных свойств, в том числе управлении сессиями, переменными, операциями, графами вычислений и устройствами. В последних разделах мы на основе полученных знаний обучили и визуализировали модель логистической регрессии и нейросеть с прямым распространением сигнала при помощи стохастического градиентного спуска. И если модель логистической сети совершала много ошибок на наборе данных MNIST, то нейросеть с прямым распространением сигнала гораздо эффективнее: в среднем всего 1,8 ошибки на 100 символов. Мы улучшим этот показатель в главе 5.

В следующей главе мы начнем работу со множеством проблем, которые возникают, когда мы делаем наши нейросети глубже. Мы уже говорили о первом элементе пазла — нахождении умных способов инициализации параметров нашей сети. Скоро вы узнаете, что, когда модели усложняются, правильной инициализации недостаточно для хороших результатов. Чтобы преодолеть эти трудности, мы углубимся в современную теорию оптимизации и создадим более совершенные алгоритмы обучения глубоких сетей.

Фундаментальные идеи в области нейросетей существуют уже десятилетия, но лишь в последнее время основанные на них модели обучения стали популярными. Наш интерес к нейросетям во многом вызван их выразительностью, которая обеспечивается многослойностью. Как мы уже говорили, глубокие нейросети способны решать проблемы, к которым раньше было невозможно даже подступиться.