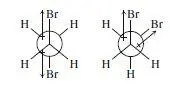
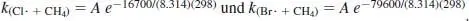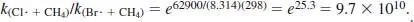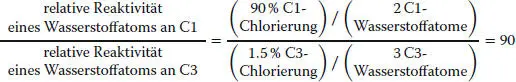Der Raumanspruch von Br ist zwar geringer als der von CH 3, aber durch die polare C–Br-Bindung entstehen im Molekül Regionen mit positiver und negativer Partialladung. Wie die nachstehenden Strukturen zeigen, haben die positiven Enden der beiden C–Br-Bindungsdipole in der gauche - und in der anti -Konformation ähnliche Abstände. In der gauche -Konformation stehen die negativen Enden dieser Dipole jedoch viel näher zusammen als in der anti -Form. Die Abstoßung zwischen diesen beiden relativ hohen Konzentrationen negativer Ladung in der Nähe der Bromatome führt zu einem Energieanstieg in der gauche -Form, der über das rein sterisch verursachte Maß hinausgeht. Daher ist die anti -Form stärker begünstigt als sonst der Fall wäre.
1 (a) CH4 + 2O2 → CO2 + 2 H2O
2 (b) C3H8 + 5O2 → 3 CO2 + 4 H2O
3 (c) C6H12 + 9O2 → 6 CO2 + 6 H2O
4 (d) C2H6O + 3 O2 → 2 CO2 + 3 H2O
5 (e) C12H22O11 + 12 O2 → 12 CO2 + 11 H2O
1 (a) C3H6O + 4 O2 → 3 CO2 + 3 H2O
2 (b) Der Energieunterschied ist die Differenz zwischen den Verbrennungswärmen: 25.9 kJ/mol; bei der Verbrennung von Aceton wird weniger Wärme frei, daher muss es zu Beginn den geringeren Energieinhalt gehabt haben.
3 (c) Aceton mit dem geringeren Energieinhalt ist die stabilere Verbindung.
Sie müssen für Sulfurylchlorid, SO 2Cl 2, einen Bindungsbruch vorschlagen, der zum gleichen Ziel führt wie der Bruch der Cl–Cl-Bindung in Cl 2. Dafür gibt es nur eine Möglichkeit: eine Schwefel-Chlor-Bindung.
Kettenstart:
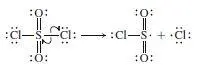
Kettenfortpflanzung:
1 (1)
2 (2)
Solange wir keinen anderen Fortpflanzungsschritt finden, um die Kettenreaktion mit 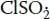 fortzusetzen, stecken wir fest. Es gibt zwei Möglichkeiten, und mit den gegebenen Informationen sind beide Vorschläge vernünftig.
fortzusetzen, stecken wir fest. Es gibt zwei Möglichkeiten, und mit den gegebenen Informationen sind beide Vorschläge vernünftig.
1 (i) Unimolekularer Zerfall von ; d. h.gefolgt von einem erneuten Fortpflanzungsschritt (1) oder
2 (ii) ein anderer Fortpflanzungsschritt, der in Schritt (1) SO2Cl· anstelle von Cl· nutzt:Beide sind qualitativ vernünftige mechanistische Möglichkeiten, auch wenn (i) wahrscheinlicher ist.
Nach Abschn. 3.4 des Lehrbuchs gilt für die Reaktion von Cl· mit CH 4: Ea = 16.7 kJ/mol = 16 700 J/mol. Daraus folgt
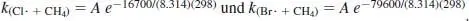
Also ist
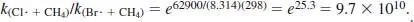
Das ist ein recht großes Geschwindigkeitsverhältnis.
Wie das Beispiel der Reaktion von Methan mit einem Gemisch aus Br 2und Cl 2sowie die Rechnung zur vorherigen Übung 3.37 gezeigt haben, sind in diesem Fall nur die Reaktionen von Cl·-Atomen mit Propan kinetisch brauchbare Fortpflanzungsschritte. Reaktionen von Br·-Atomen sind viel zu langsam, um konkurrieren zu können. Dieser erste Schritt bestimmt das Verhältnis, in dem sich primäre und sekundäre Alkylradikale bilden. Die beobachtete Selektivität ist demnach die der Cl·-Atome. Beide Radikale reagieren mit den beiden molekularen Halogenen Cl 2und Br 2sehr rasch weiter. Da das Verhältnis der vorhandenen Radikale im vorherigen Schritt bestimmt wurde, sind die Isomerenverhältnisse der entstandenen Chlorpropane und Brompropane im Wesentlichen gleich und geben die Selektivität der Chlorierung wieder.
1 (a) Kettenstart: Bruch der schwächsten Bindung, das ist die O–O-Bindung, unter Bildung von Hydroxyl-Radikalen.Fortpflanzungsschritte (PS): Verwenden Sie wie bei der Halogenierung die im Kettenstart gebildete Spezies, um ein Wasserstoffatom vom Substrat abzuziehen. Setzen Sie die Reaktion fort bis zu den Endprodukten.Kettenabbruchschritte: Kombinieren Sie alle möglichen Paare der Radikale.
2 (b) Es gibt zwei Möglichkeiten: Entweder (i) Sie addieren die ΔH° -Werte der beiden Fortpflanzungsschritte (einfacher) oder (ii) Sienutzen die stöchiometrische Gleichung und kombinieren alle ΔH°-Werte:(i) (–59) + (–176) = –235 kJ/mol(ii) CH4 + HOOH → CH3OH + HOH
3 (c) Der ΔH°-Wert dieser Reaktion ist sehr viel negativer, daher ist sie thermodynamisch bei weitem günstiger.
4 (d) Wie bei der Halonierung ist der erste Fortpflanzungsschritt auch bei dieser Reaktion geschwindigkeitsbestimmend. Die Gesamtreaktion ist aber merkwürdigerweise langsamer, obwohl der erste Fortpflanzungsschritt exotherm ist, weil er eine größere Aktivierungsenergie hat der erste Fortpflanzungsschritt der Chlorierung.
Gehen Sie bei der Berechnung nach der gleichen Methode vor wie in Abschn. 3.6 beschrieben. Es gibt drei Gruppen von Wasserstoffatomen mit unterschiedlichen Reaktivitäten: zwei an C1, zwei an C2 und drei an C3. Den relativen Ausbeuten zufolge scheinen diejenigen an C3 die geringste Reaktivität zu haben. Daher ist es sinnvoll zu berechnen, wie viel reaktiver die Wasserstoffatome an C2 und C1 gegenüber denen an C3 sind. Vergleichen wir zuerst C2 und C3:

Und nun C1 mit C3:
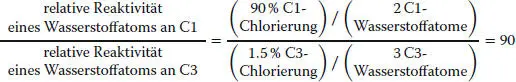
Im Fall von Propan (Abschn. 3.6) waren die Wasserstoffatome an C2 (sekundär) etwa 4-mal reaktiver als die an C1 oder C3 (primär), weil sekundäre Alkylradikale stabiler sind als primäre. Bei der Verbindung dieser Aufgabe, 1-Brompropan, sind die Wasserstoffatome am Br-substituierten C1 am reaktivsten. Offenbar wird das Radikal an C1 durch das Bromatom stark stabilisiert. Eine vernünftig Annahme ist, dass diese Stabilisierung mit den freien Elektronenpaaren am Bromatom zusammenhängt, denn wir wissen, dass Radikale elektronenarm sind: Sie werden in Alkanen durch Hyperkonjugation stabilisiert, wobei Elektronen aus benachbarten Bindungen zum halb besetzten p -Orbital des Radikals delokalisieren. Bei 1-Brompropan kann man sich vorstellen, dass sich ein p -Orbital des Bromatoms mit freiem Elektronenpaar und das halb besetzte p -Orbital des Kohlenstoffatoms ausrichten und überlappen; diese Überlappung kann auch als Resonanz dargestellt werden:
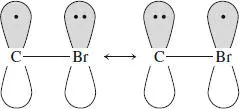
Alle benötigten DH° -Werte stehen in Tab. 3.1, nur für X–X sind sie in Tab. 3.4 angegeben.
1 (a) Mit ΔH° = DH°(gelöste Bindung) – DH°(geknüpfte Bindung) erhält man folgende Antworten (in kJ/mol):ReaktionΔH◦ für X = FClBrI(1)HX· + CH4 → CH3X + HH·–21+84+142+201(2)H· + X2 → HX· + X–411–189–172–147(1) + (2)CH4 + X2 → CH3X + HXΔH◦ = −432–105–30+54
Читать дальше


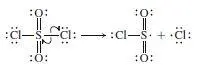
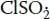 fortzusetzen, stecken wir fest. Es gibt zwei Möglichkeiten, und mit den gegebenen Informationen sind beide Vorschläge vernünftig.
fortzusetzen, stecken wir fest. Es gibt zwei Möglichkeiten, und mit den gegebenen Informationen sind beide Vorschläge vernünftig.