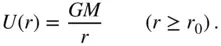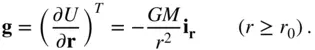(2.121) 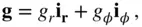
where
(2.122) 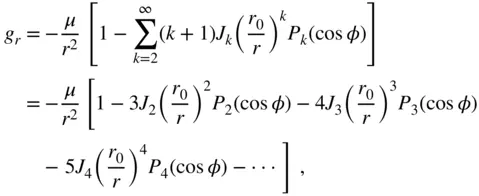
and
(2.123) 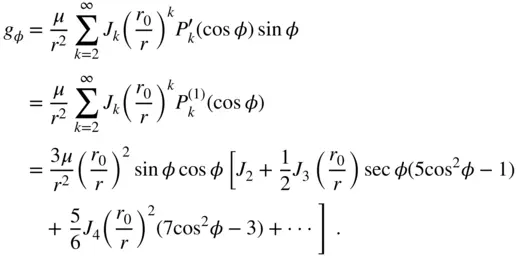
Due to a non‐zero transverse gravity component, 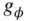 , the direction of
, the direction of 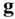 differs from the radial direction, while its radial component,
differs from the radial direction, while its radial component, 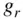 , is smaller in magnitude when compared to that predicted by a spherical gravity model; that is, the model derived by assuming a perfectly spherical mass distribution of a body of radius
, is smaller in magnitude when compared to that predicted by a spherical gravity model; that is, the model derived by assuming a perfectly spherical mass distribution of a body of radius 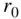 .
.
2.7.4 Spherical Body with Radially Symmetric Mass Distribution
A spherical body of constant radius 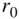 with a radially symmetrical mass distribution has the density
with a radially symmetrical mass distribution has the density 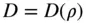 , varying only with the radius,
, varying only with the radius, 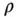 . A body consisting of concentric spherical shells, each of which has a different (either constant or radially varying) density, has a radially symmetrical mass distribution. Such a distribution results in the vanishing of all the integrals of
. A body consisting of concentric spherical shells, each of which has a different (either constant or radially varying) density, has a radially symmetrical mass distribution. Such a distribution results in the vanishing of all the integrals of 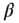 and
and 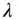 in Eqs. ( 2.109)–( 2.111), which produces
in Eqs. ( 2.109)–( 2.111), which produces 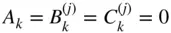 , thereby implying a potential which is independent of the co‐latitude and longitude. Hence the gravitational potential of a body with a spherically symmetric mass distribution of radius,
, thereby implying a potential which is independent of the co‐latitude and longitude. Hence the gravitational potential of a body with a spherically symmetric mass distribution of radius, 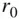 , is given by
, is given by
(2.124) 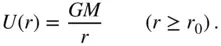
Clearly, a spherical body with a radially symmetric mass distribution behaves exactly as if all its mass were concentrated at its centre. The acceleration due to gravity is thus given by
(2.125) 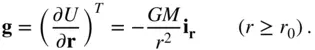
1 A particle, , is launched vertically upward with velocity, , from the surface of a spherical planet of radius , rotating about the polar axis, , from west to east at the rate . The launch takes place at the latitude, , and longitude, , measured from a fixed meridian, , as shown in Fig. 2.6. Derive the expressions for the net velocity and acceleration of the particle, and resolve the vector components in a reference frame, , with its origin, , at the centre of the planet, and with one axis along the polar axis, , another along the meridian, , and the third axis, , normal to both and . Figure 2.6Geometry for Exercise 1.
2 A point, , moves on the horizontal plane, , describing a circle of radius around the centroid, , of a cylinder of length and radius , which is rotating about the axis, , at a constant angular speed, , as shown in Fig. 2.7. The angle made by the line with the axis is , which varies with time at a constant rate, . Another point, , is on the edge of the cylinder at its base, , located at the semi‐length, , from the median section, . The radial line, , makes an angle, , with the vertical axis, , passing through (Fig. 2.7). Derive the expressions for the position, velocity, and acceleration vectors of relative to as functions of time, , assuming that when , and resolve the components in the reference frame, , with the mutually perpendicular axes, , , and , shown in Fig. 2.7. Figure 2.7Geometry for Exercise 2.
3 Transform the equations of motion of the system of particles under mutual gravitational attraction to the following generalized coordinates, , of Lagrange:and show that they can be expressed as follows:where is the Lagrangian of the system, with and being the net kinetic and potential energies.
4 Transform the system of equations derived in Exercise 3 to a set of variables, , called the generalized momenta, defined byand show that they can be expressed in the following canonical form (Whittaker, 1988):where the net kinetic energy, , is expressed as follows:andis the Hamiltonian of the system, with being the net potential energy.
5 Referring to Exercise 4, show that if the Hamiltonian is not explicitly dependent on the time, , i.e.,then we haveor .
6 Consider four particles, each having the mass, , such that three of them are always located at the vertices of an equilateral triangle while the fourth is at its centroid. What is the angular velocity, , of the triangle?
7 Derive an expression for the gravitational potential of a thin circular ring of uniform density with mass, , radius, , and negligible cross‐sectional area, at a point located on the plane of the ring at radius from the centre, where (a) , and (b) . (Ans. (a) .)
8 Calculate the gravitational potential of a thin spherical shell of radius, and constant density per unit surface area, , at a point located at radius from the centre, where (a) , and (b) .
9 The density of a spherically symmetric mass distribution extending up to a radius is given bywhere is a constant. Find the gravitational potential for , as well as the net potential energy, if the total mass of the distribution is .
1 Whittaker ET 1988. Analytical Dynamics of Particles and Rigid Bodies. Cambridge University Press, New York.
2 Abramowitz M and Stegun IA 1974. Handbook of Mathematical Functions. Dover, New York.
1 1A reference frame, , consisting of three mutually perpendicular axes, , and , is termed a right‐handed frame if it satisfies the right‐hand rule of vector multiplication of the first two axes in the proper sequence, to produce the third axis:
2 2This caveat must be added because, as postulated by Einstein in 1905, Newton's laws cease to apply to objects travelling close to the speed of light, which is the same in all reference frames.
3 3Rotation of the frame, , refers to the rotation of its axes. Since , and are unit vectors, they cannot change in magnitude. Hence the time derivative of each axis is just due to its rotation by an angular velocity, . This angular velocity is common to all axes because they must always be mutually perpendicular and right handed. Therefore, we have
Читать дальше

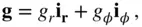
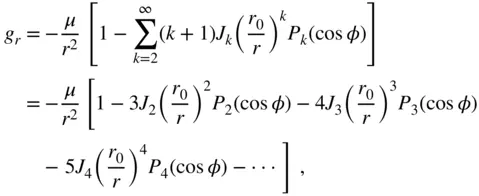
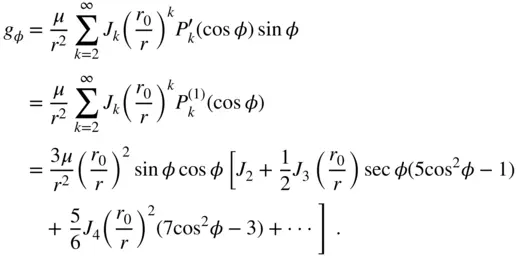
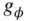 , the direction of
, the direction of 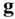 differs from the radial direction, while its radial component,
differs from the radial direction, while its radial component, 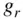 , is smaller in magnitude when compared to that predicted by a spherical gravity model; that is, the model derived by assuming a perfectly spherical mass distribution of a body of radius
, is smaller in magnitude when compared to that predicted by a spherical gravity model; that is, the model derived by assuming a perfectly spherical mass distribution of a body of radius 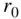 .
.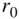 with a radially symmetrical mass distribution has the density
with a radially symmetrical mass distribution has the density 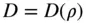 , varying only with the radius,
, varying only with the radius, 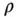 . A body consisting of concentric spherical shells, each of which has a different (either constant or radially varying) density, has a radially symmetrical mass distribution. Such a distribution results in the vanishing of all the integrals of
. A body consisting of concentric spherical shells, each of which has a different (either constant or radially varying) density, has a radially symmetrical mass distribution. Such a distribution results in the vanishing of all the integrals of 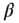 and
and 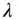 in Eqs. ( 2.109)–( 2.111), which produces
in Eqs. ( 2.109)–( 2.111), which produces 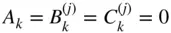 , thereby implying a potential which is independent of the co‐latitude and longitude. Hence the gravitational potential of a body with a spherically symmetric mass distribution of radius,
, thereby implying a potential which is independent of the co‐latitude and longitude. Hence the gravitational potential of a body with a spherically symmetric mass distribution of radius, 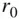 , is given by
, is given by