(2.102) 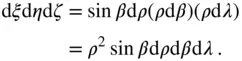
If the mass density at the location of the elemental mass is given by 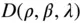 , then the elemental mass is the following:
, then the elemental mass is the following:
(2.103) 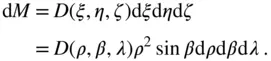
The angle 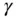 between
between 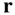 , and
, and  (Fig. 2.4) is related to the spherical coordinates by the following cosine law of the scalar product of two vectors:
(Fig. 2.4) is related to the spherical coordinates by the following cosine law of the scalar product of two vectors:
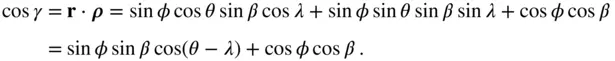
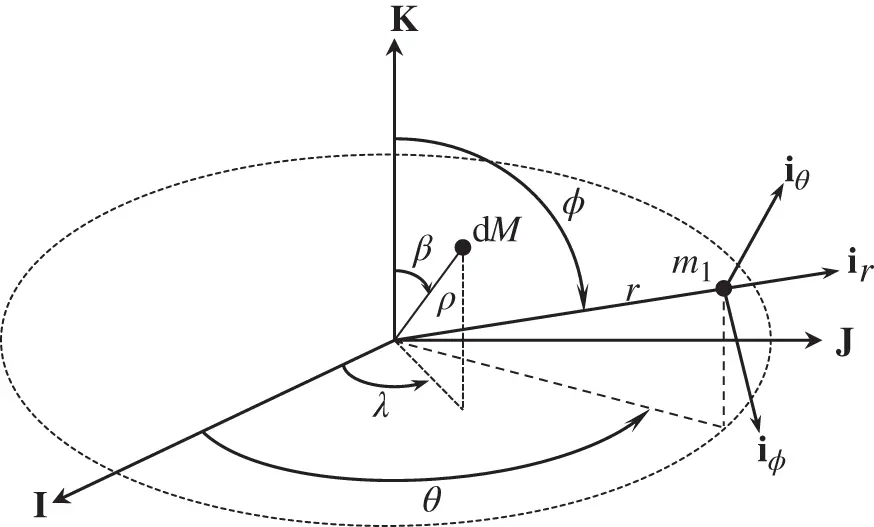
Figure 2.5Spherical coordinates for the gravitational potential of a body.
To derive the gravitational potential given by Eq. (2.94)in spherical coordinates, it is necessary to expand the cosine law ( Eq. 2.104) in terms of the Legendre polynomials. To do so, consider the following associated Legendre functions of the first kind, degree 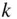 and order
and order 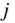 (Abramowitz and Stegun 1974):
(Abramowitz and Stegun 1974):
(2.104) 
where  is the Legendre polynomial of degree
is the Legendre polynomial of degree  . Some of the commonly used associated Legendre functions are
. Some of the commonly used associated Legendre functions are
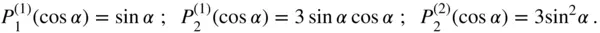
In terms of the associated Legendre functions and the Legendre polynomials of the first degree, Eq. 2.104becomes
(2.105) 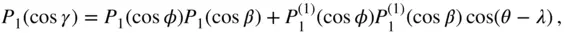
which is referred to as the addition theorem for the Legendre polynomials of the first degree, 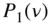 . In terms of the Legendre polynomials of the second degree,
. In terms of the Legendre polynomials of the second degree, 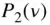 , we have
, we have
(2.106) 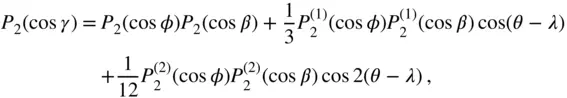
which is the addition theorem for the Legendre polynomials of the second degree, 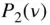 . Extending this procedure leads to the following addition theorem for the Legendre polynomials of degree
. Extending this procedure leads to the following addition theorem for the Legendre polynomials of degree 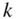 ,
, 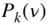 :
:
(2.107) 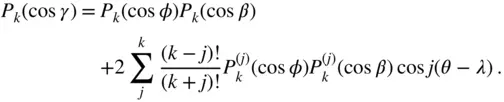
The substitution of the addition theorem into Eq. (2.94)results in the following expansion of the gravitational potential:
(2.108) 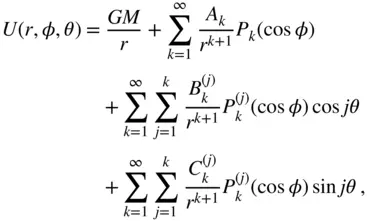
where
(2.109) 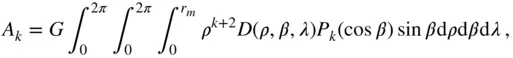
(2.110) 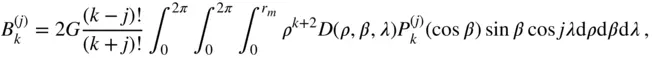
(2.111) 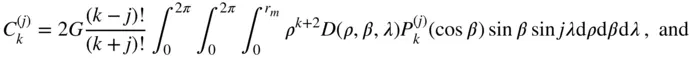
with 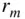 denoting the maximum radial extent of the body. The mass of the body is evaluated by
denoting the maximum radial extent of the body. The mass of the body is evaluated by
(2.112) 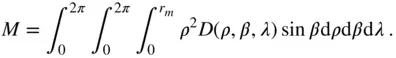
Equation ( 2.108) is a general expansion of the gravitational potential which can be applied to a body of an arbitrary shape and an arbitrary mass distribution. However, the evaluation of the series coefficients by Eqs. ( 2.109)–( 2.111) is often a difficult exercise for a body of a complicated shape, and requires experimental determination (such as the acceleration measurements by a low‐orbiting satellite).
A body whose mass is symmetrically distributed about the polar axis, 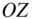 , has its density varying only with the radius and the latitude; that is,
, has its density varying only with the radius and the latitude; that is, 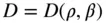 . Upon neglecting the longitudinal
. Upon neglecting the longitudinal  variations in the mass distribution, the additional theorem for the Legendre polynomial of degree
variations in the mass distribution, the additional theorem for the Legendre polynomial of degree 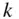 , Eq. (2.107), becomes the following:
, Eq. (2.107), becomes the following:
Читать дальше

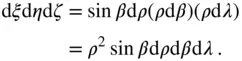
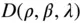 , then the elemental mass is the following:
, then the elemental mass is the following: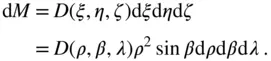
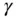 between
between 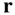 , and
, and  (Fig. 2.4) is related to the spherical coordinates by the following cosine law of the scalar product of two vectors:
(Fig. 2.4) is related to the spherical coordinates by the following cosine law of the scalar product of two vectors: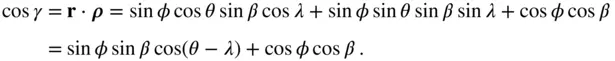

 and order
and order  (Abramowitz and Stegun 1974):
(Abramowitz and Stegun 1974):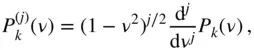
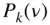 is the Legendre polynomial of degree
is the Legendre polynomial of degree 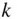 . Some of the commonly used associated Legendre functions are
. Some of the commonly used associated Legendre functions are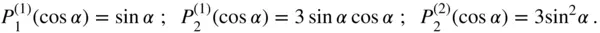
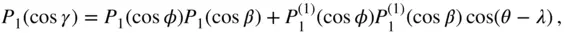
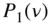 . In terms of the Legendre polynomials of the second degree,
. In terms of the Legendre polynomials of the second degree, 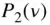 , we have
, we have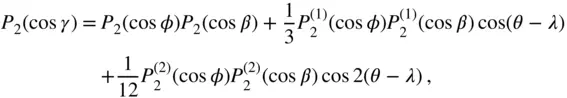
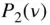 . Extending this procedure leads to the following addition theorem for the Legendre polynomials of degree
. Extending this procedure leads to the following addition theorem for the Legendre polynomials of degree 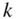 ,
, 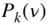 :
: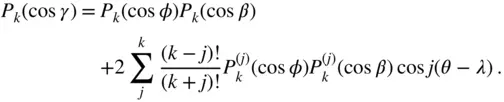
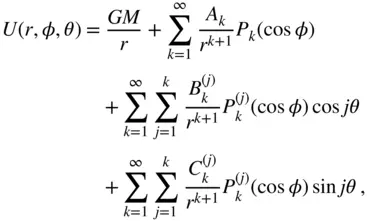
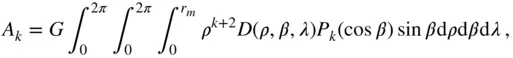
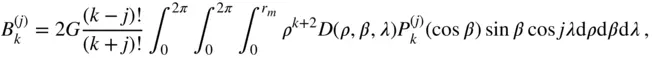
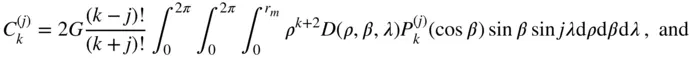
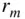 denoting the maximum radial extent of the body. The mass of the body is evaluated by
denoting the maximum radial extent of the body. The mass of the body is evaluated by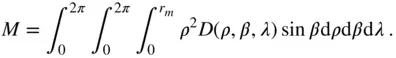
 , has its density varying only with the radius and the latitude; that is,
, has its density varying only with the radius and the latitude; that is, 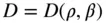 . Upon neglecting the longitudinal
. Upon neglecting the longitudinal 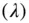 variations in the mass distribution, the additional theorem for the Legendre polynomial of degree
variations in the mass distribution, the additional theorem for the Legendre polynomial of degree  , Eq. (2.107), becomes the following:
, Eq. (2.107), becomes the following:










