Ashish Tewari - Foundations of Space Dynamics

(2.65)

where

(2.66)

is the total potential energy of the system,

(2.67)

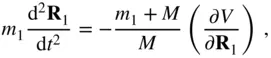
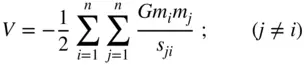
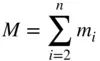
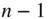is the mass of the body consisting of the last particles,

(2.68)

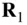with being the location of the test mass , 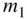, in an inertial reference frame, ( OXYZ ), and 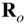being the location of the centre of mass of the attracting body consisting of the remaining 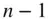particles, which are located at 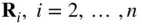. If it is further assumed that the test mass is negligible in comparison with the combined mass of the remaining 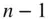particles constituting the body, that is, 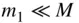, then the test mass, 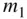, causes a negligible acceleration on the body. Consequently, the body can be assumed to be at rest, and the origin of the inertial reference frame, OXYZ , is moved to the centre of mass of the body, i.e., 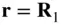, , 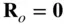and 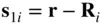. Hence, the equation of motion of the test mass becomes the following: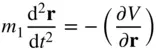

(2.69)

or, since the partial derivative on the right‐hand side yields only the terms for which either or equals 1, we have

(2.70)

In terms of the gravitational potential of the body at the location of the test mass, which is given by

(2.71)

the acceleration of the test mass is expressed by dividing the right‐hand side of Eq. (2.70)by as follows: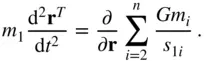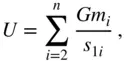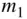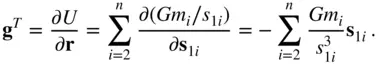

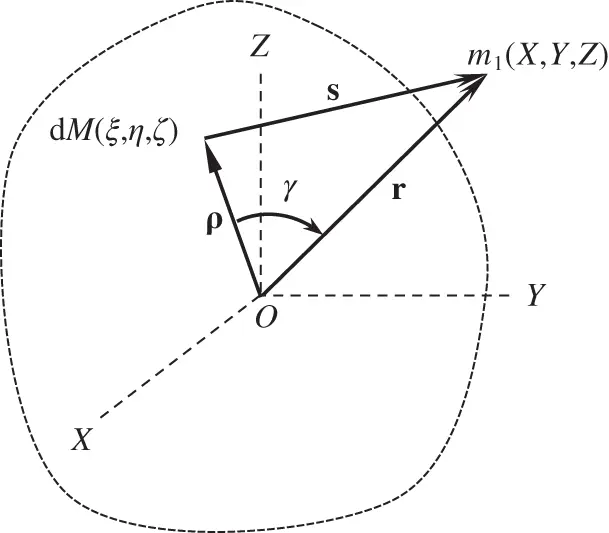
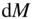(2.72)

Figure 2.4An elemental mass, , of a body with centre of mass O , and a test mass, 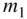, located away from the body.

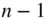For all the particles constituting the mass, M , of the attracting body, let the limit of an infinitesimal elemental mass , 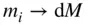, be taken as 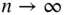, whereby the summation in Eq. (2.71)is replaced by the following integral: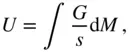

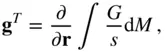
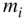(2.73)

which results in the following expression for the acceleration of the test mass:

(2.74)

where s is the distance of the test mass, , from the elemental mass, 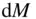, as depicted in Fig. 2.4, and can be expressed as follows: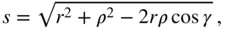

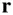(2.75)

with and 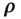being the position vectors of the test mass, 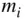, and the elemental mass, 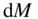, respectively, from the centre of mass of the attracting body, and 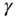, being the angle between 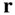, and 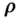as shown in Fig. 2.4.