(2.89) 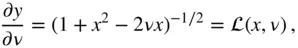
or
(2.90) 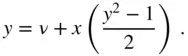
Since 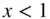 , the following series expansion (called Lagrange's expansion theorem ) can be applied to Eq. (2.90)(Abramowitz and Stegun 1974):
, the following series expansion (called Lagrange's expansion theorem ) can be applied to Eq. (2.90)(Abramowitz and Stegun 1974):
(2.91) 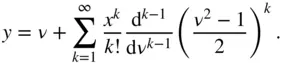
The differentiation of Eq. (2.91)with 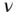 results in
results in
(2.92) 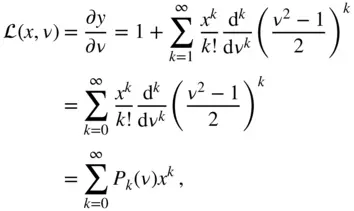
where 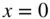 corresponds to the root
corresponds to the root 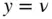 . Equation ( 2.92) yields the following expression for the Legendre polynomials, called Rodrigues' formula :
. Equation ( 2.92) yields the following expression for the Legendre polynomials, called Rodrigues' formula :
(2.93) 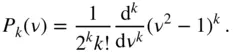
The gravitational potential is expressed as follows in terms of the Legendre polynomials by substituting Eq. (2.81)into Eq. (2.78):
(2.94) 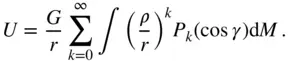
It is possible to further simplify the gravitational potential before carrying out the complete integration. The integral arising out of 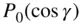 in Eq. (2.94)yields the mass, M , of the planet, thereby resulting in
in Eq. (2.94)yields the mass, M , of the planet, thereby resulting in
(2.95) 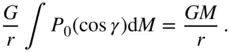
2.7.2 Spherical Coordinates
To evaluate the gravitational potential given by Eq. (2.94), it is necessary to introduce the spherical coordinates for the mass distribution of the body, as well as the location of the test mass. Let the right‐handed triad, 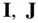 , and
, and 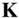 , represent the axes,
, represent the axes, 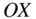 ,
, 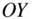 , and
, and 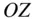 , respectively, of the inertial frame, ( OXYZ ), with the origin,
, respectively, of the inertial frame, ( OXYZ ), with the origin, 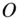 , at the centre of the body. The location of the test mass,
, at the centre of the body. The location of the test mass, 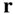 , is resolved in the spherical coordinates,
, is resolved in the spherical coordinates, 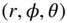 , as follows (Fig. 2.5):
, as follows (Fig. 2.5):
(2.96) 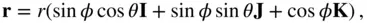
where 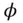 is the co‐latitude and
is the co‐latitude and 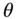 is the longitude . Similarly, let an elemental mass,
is the longitude . Similarly, let an elemental mass, 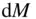 , on the body be located by
, on the body be located by 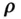 using the spherical coordinates
using the spherical coordinates 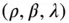 as follows (Fig. 2.5):
as follows (Fig. 2.5):
(2.97) 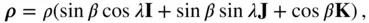
where 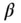 and
and 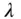 are the co‐latitude and longitude, respectively, of the elemental mass.
are the co‐latitude and longitude, respectively, of the elemental mass.
The coordinate transformation between the spherical and Cartesian coordinates for the elemental mass is the following:
(2.98) 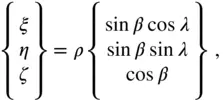
differentiating which produces
(2.99) 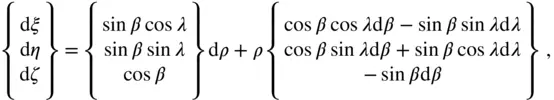
or the following in the matrix form:
(2.100) 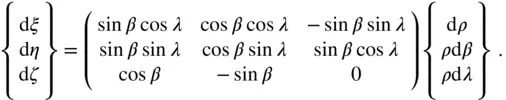
An inversion of the square matrix on the right‐hand side (called the Jacobian of the coordinate transformation) yields the following result:
(2.101) 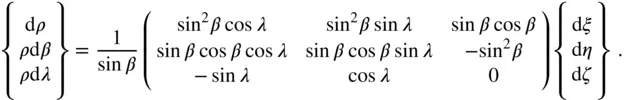
Since the determinant of the matrix on the right‐hand side of Eq. (2.100)equals 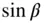 , and that of the inverse matrix in Eq. (2.101)is
, and that of the inverse matrix in Eq. (2.101)is 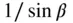 , the two sets of coordinates are related by the following expression for the elemental volume at
, the two sets of coordinates are related by the following expression for the elemental volume at 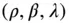 :
:
Читать дальше

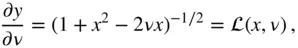
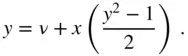
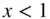 , the following series expansion (called Lagrange's expansion theorem ) can be applied to Eq. (2.90)(Abramowitz and Stegun 1974):
, the following series expansion (called Lagrange's expansion theorem ) can be applied to Eq. (2.90)(Abramowitz and Stegun 1974):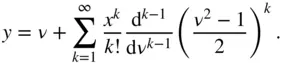
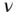 results in
results in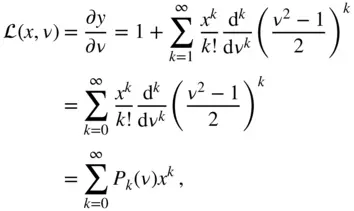
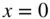 corresponds to the root
corresponds to the root 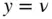 . Equation ( 2.92) yields the following expression for the Legendre polynomials, called Rodrigues' formula :
. Equation ( 2.92) yields the following expression for the Legendre polynomials, called Rodrigues' formula :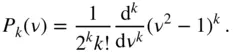
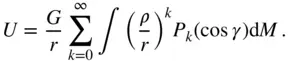
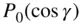 in Eq. (2.94)yields the mass, M , of the planet, thereby resulting in
in Eq. (2.94)yields the mass, M , of the planet, thereby resulting in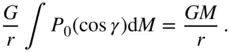
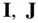 , and
, and 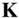 , represent the axes,
, represent the axes, 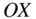 ,
, 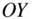 , and
, and 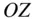 , respectively, of the inertial frame, ( OXYZ ), with the origin,
, respectively, of the inertial frame, ( OXYZ ), with the origin, 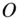 , at the centre of the body. The location of the test mass,
, at the centre of the body. The location of the test mass, 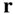 , is resolved in the spherical coordinates,
, is resolved in the spherical coordinates, 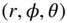 , as follows (Fig. 2.5):
, as follows (Fig. 2.5):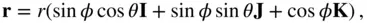
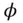 is the co‐latitude and
is the co‐latitude and 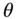 is the longitude . Similarly, let an elemental mass,
is the longitude . Similarly, let an elemental mass, 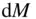 , on the body be located by
, on the body be located by 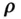 using the spherical coordinates
using the spherical coordinates 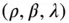 as follows (Fig. 2.5):
as follows (Fig. 2.5):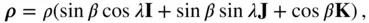
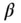 and
and 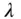 are the co‐latitude and longitude, respectively, of the elemental mass.
are the co‐latitude and longitude, respectively, of the elemental mass.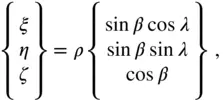
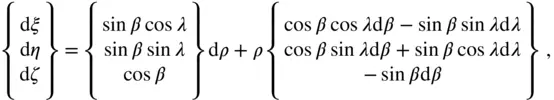
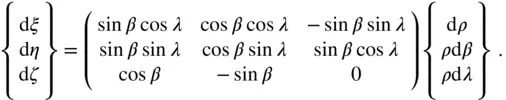
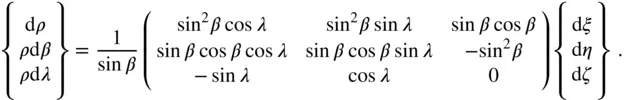
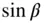 , and that of the inverse matrix in Eq. (2.101)is
, and that of the inverse matrix in Eq. (2.101)is 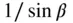 , the two sets of coordinates are related by the following expression for the elemental volume at
, the two sets of coordinates are related by the following expression for the elemental volume at 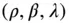 :
:










