
1 Cover
2 Foundations of Space Dynamics Foundations of Space Dynamics First Edition Ashish Tewari Indian Institute of Technology Kanpur
3 Aerospace Series – Recently Published Titles
4 Copyright
5 dedication-page
6 Preface
7 1 Introduction 1.1 Space Flight 1.2 Reference Frames and Time Scales 1.3 Classification of Space Missions Exercises References Note
8 2 Dynamics 2.1 Notation and Basics 2.2 Plane Kinematics 2.3 Newton's Laws 2.4 Particle Dynamics 2.5 The n‐Body Problem 2.6 Dynamics of a Body 2.7 Gravity Field of a Body Exercises References Notes
9 Chapter 3: Keplerian Motion 3.1 The Two‐Body Problem 3.2 Orbital Angular Momentum 3.3 Orbital Energy Integral 3.4 Orbital Eccentricity 3.5 Orbit Equation 3.6 Orbital Velocity and Flight Path Angle 3.7 Perifocal Frame and Lagrange's Coefficients Exercises Notes
10 Chapter 4: Time in Orbit 4.1 Position and Velocity in an Elliptic Orbit 4.2 Solution to Kepler's Equation 4.3 Position and Velocity in a Hyperbolic Orbit 4.4 Position and Velocity in a Parabolic Orbit 4.5 Universal Variable for Keplerian Motion Exercises References
11 5 Orbital Plane 5.1 Rotation Matrix 5.2 Euler Axis and Principal Angle 5.3 Elementary Rotations and Euler Angles 5.4 Euler‐Angle Representation of the Orbital Plane 5.5 Planet‐Fixed Coordinate System
12 6 Orbital Manoeuvres 6.1 Single‐Impulse Orbital Manoeuvres 6.2 Multi‐impulse Orbital Transfer 6.3 Continuous Thrust Manoeuvres Exercises References
13 7 Relative Motion in Orbit 7.1 Hill‐Clohessy‐Wiltshire Equations 7.2 Linear State‐Space Model 7.3 Impulsive Manoeuvres About a Circular Orbit 7.4 Keplerian Relative Motion Exercises
14 8 Lambert's Problem 8.1 Two‐Point Orbital Transfer 8.2 Elliptic Transfer 8.3 Lambert's Theorem 8.4 Solution to Lambert's Problem Exercises References
15 9 Orbital Perturbations 9.1 Perturbing Acceleration 9.2 Osculating Orbit 9.3 Variation of Parameters 9.4 Lagrange Planetary Equations 9.5 Gauss Variational Model 9.6 Variation of Vectors 9.7 Mean Orbital Perturbation 9.8 Orbital Perturbation Due to Oblateness 9.9 Effects of Atmospheric Drag 9.10 Third‐Body Perturbation 9.11 Numerical Methods for Perturbed Keplerian Motion Exercises References
16 10 Three‐Body Problem 10.1 Equations of Motion 10.2 Particular Solutions by Lagrange 10.3 Circular Restricted Three‐Body Problem 10.4 Non‐dimensional Equations in the Synodic Frame 10.5 Lagrangian Points and Stability 10.6 Orbital Energy and Jacobi's Integral 10.7 Canonical Formulation 10.8 Special Three‐Body Trajectories Exercises Reference
17 11 Attitude Dynamics 11.1 Euler's Equations of Attitude Kinetics 11.2 Attitude Kinematics 11.3 Rotational Kinetic Energy 11.4 Principal Axes 11.5 Torque‐Free Rotation of Spacecraft 11.6 Precession and Nutation 11.7 Semi‐Rigid Spacecraft 11.8 Solution to Torque‐Free Euler's Equations 11.9 Gravity‐Gradient Stabilization Exercises
18 12 Attitude Manoeuvres 12.1 Impulsive Manoeuvres with Attitude Thrusters 12.2 Attitude Manoeuvres with Rotors Exercises References
19 ANumerical Solution of Ordinary Differential Equations A.1 Fixed‐Step Runge‐Kutta Algorithms A.2 Variable‐Step Runge‐Kutta Algorithms A.3 Runge‐Kutta‐Nyström Algorithms References
20 BJacobian Elliptic Functions Reference
21 Index
22 End User License Agreement
1 Chapter 1 Table 1.1 Variation of density with altitude in Earth's atmosphere
2 Chapter 3Table 3.1 Two‐body orbits.
3 Chapter 4Table 4.1 Iteration steps for the solution of Kepler's equation by Newton's m...Table 4.2 Bessel functions of the first kind and order 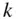 .Table 4.3 Iteration steps for the solution of the hyperbolic Kepler's equatio...Table 4.4 Iteration steps for the solution of the universal Kepler's equation...
.Table 4.3 Iteration steps for the solution of the hyperbolic Kepler's equatio...Table 4.4 Iteration steps for the solution of the universal Kepler's equation...
4 Chapter 6Table 6.1 The specific impulse, 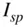 , of some chemical rocket propellants
, of some chemical rocket propellants
5 Chapter 7Table 7.1 Comparison of relative position and velocity in a geosynchronous or...
6 Chapter 8Table 8.1 Time of flight, 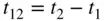 , for a transfer between
, for a transfer between 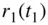 and
and 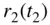 with a chord lengt...
with a chord lengt...
7 Chapter 9Table 9.1 Non‐zero Lagrange brackets for a perturbed elliptic orbit.Table 9.2 The oblateness parameter, 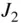 , of some major bodies.Table 9.3 The inclination angle for Sun‐synchronous spacecraft in circular or...Table 9.4 Mass ratio to the solar mass, average distance from the sun, and th...
, of some major bodies.Table 9.3 The inclination angle for Sun‐synchronous spacecraft in circular or...Table 9.4 Mass ratio to the solar mass, average distance from the sun, and th...
8 1Table A.1 Coefficients of the Runge‐Kutta 4(5) algorithm
1 Chapter 1 Figure 1.1 Decay in the orbit due to atmospheric drag for a spacecraft initi... Figure 1.2 Decay in the orbit due to atmospheric drag for a spacecraft initi... Figure 1.3 The equinoctial sidereal frame 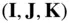 , the ecliptic synodic frame
, the ecliptic synodic frame 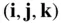 , a...
, a...
2 Chapter 2 Figure 2.1 The position vector, 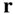 , of a particle resolved in an inertial ref... Figure 2.2 A system of
, of a particle resolved in an inertial ref... Figure 2.2 A system of 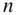 particles in an inertial reference frame OXYZ . Figure 2.3 A body as a collection of large number of particles of elemental ... Figure 2.4 An elemental mass,
particles in an inertial reference frame OXYZ . Figure 2.3 A body as a collection of large number of particles of elemental ... Figure 2.4 An elemental mass, 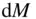 , of a body with centre of mass O , and a test... Figure 2.5 Spherical coordinates for the gravitational potential of a body.... Figure 2.6 Geometry for Exercise 1. Figure 2.7 Geometry for Exercise 2.
, of a body with centre of mass O , and a test... Figure 2.5 Spherical coordinates for the gravitational potential of a body.... Figure 2.6 Geometry for Exercise 1. Figure 2.7 Geometry for Exercise 2.
3 Chapter 3 Figure 3.1 Two spherical bodies in mutual gravitational attraction. Figure 3.2 Orbital angular momentum and the constant orbital plane.Figure 3.3 The conic section shapes of a non‐rectilinear Keplerian orbit.Figure 3.4 The elliptic orbit 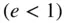 .Figure 3.5 The parabolic orbit
.Figure 3.5 The parabolic orbit 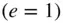 .Figure 3.6 The hyperbolic orbit
.Figure 3.6 The hyperbolic orbit 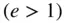 .Figure 3.7 The orbital velocity vector in the local‐horizon frame.
.Figure 3.7 The orbital velocity vector in the local‐horizon frame.
4 Chapter 4Figure 4.1 The auxilliary circle and the eccentric anomaly.
Читать дальше


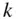 .Table 4.3 Iteration steps for the solution of the hyperbolic Kepler's equatio...Table 4.4 Iteration steps for the solution of the universal Kepler's equation...
.Table 4.3 Iteration steps for the solution of the hyperbolic Kepler's equatio...Table 4.4 Iteration steps for the solution of the universal Kepler's equation...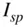 , of some chemical rocket propellants
, of some chemical rocket propellants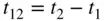 , for a transfer between
, for a transfer between 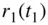 and
and 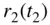 with a chord lengt...
with a chord lengt...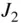 , of some major bodies.Table 9.3 The inclination angle for Sun‐synchronous spacecraft in circular or...Table 9.4 Mass ratio to the solar mass, average distance from the sun, and th...
, of some major bodies.Table 9.3 The inclination angle for Sun‐synchronous spacecraft in circular or...Table 9.4 Mass ratio to the solar mass, average distance from the sun, and th...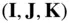 , the ecliptic synodic frame
, the ecliptic synodic frame 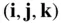 , a...
, a... , of a particle resolved in an inertial ref... Figure 2.2 A system of
, of a particle resolved in an inertial ref... Figure 2.2 A system of  particles in an inertial reference frame OXYZ . Figure 2.3 A body as a collection of large number of particles of elemental ... Figure 2.4 An elemental mass,
particles in an inertial reference frame OXYZ . Figure 2.3 A body as a collection of large number of particles of elemental ... Figure 2.4 An elemental mass, 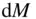 , of a body with centre of mass O , and a test... Figure 2.5 Spherical coordinates for the gravitational potential of a body.... Figure 2.6 Geometry for Exercise 1. Figure 2.7 Geometry for Exercise 2.
, of a body with centre of mass O , and a test... Figure 2.5 Spherical coordinates for the gravitational potential of a body.... Figure 2.6 Geometry for Exercise 1. Figure 2.7 Geometry for Exercise 2.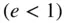 .Figure 3.5 The parabolic orbit
.Figure 3.5 The parabolic orbit 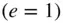 .Figure 3.6 The hyperbolic orbit
.Figure 3.6 The hyperbolic orbit 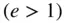 .Figure 3.7 The orbital velocity vector in the local‐horizon frame.
.Figure 3.7 The orbital velocity vector in the local‐horizon frame.










