(2.56) 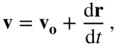
where the time derivative is taken relative to the inertial frame, ( OXYZ ). Integrated over all the mass particles constituting the body, Eq. (2.55)yields the following result:
(2.57) 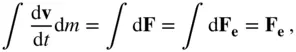
where all the internal forces (consisting of equal and opposite pairs) cancel out by Newton's third law, and 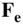 is the net external force acting on the body.
is the net external force acting on the body.
The term on the left‐hand side of Eq. (2.57)can be simplified by moving the time derivative outside the integral, because the total mass, 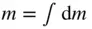 , of the body is a constant. This fact, along with Eq. (2.56), leads to the following:
, of the body is a constant. This fact, along with Eq. (2.56), leads to the following:
(2.58) 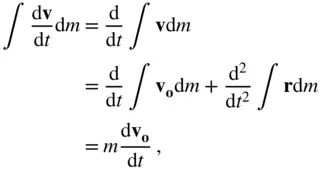
where we have 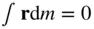 by the virtue of
by the virtue of  being the centre of mass of the body. Thus Eqs. ( 2.57) and ( 2.58) result in the following equation of the body's translation :
being the centre of mass of the body. Thus Eqs. ( 2.57) and ( 2.58) result in the following equation of the body's translation :
(2.59) 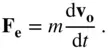
Thus the translational motion of the body is described by the motion of its centre of mass, as if all the mass were concentrated at that point.
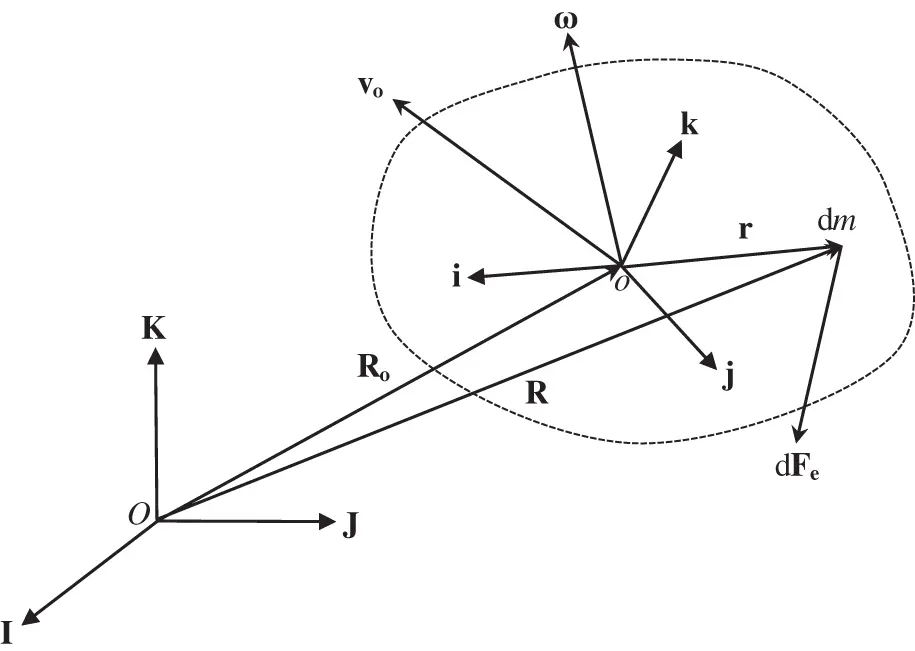
Figure 2.3A body as a collection of large number of particles of elemental mass, 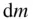 , with centre of mass o .
, with centre of mass o .
The rotational kinetics of the body are described by taking moments of Eq. (2.55)about the centre of mass, 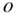 , and integrating over the body as follows:
, and integrating over the body as follows:
(2.60) 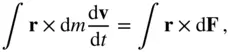
where all the internal torques cancel out (being equal and opposite pairs), resulting in only the net external torque, 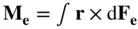 , appearing on the right‐hand side. The left‐hand side of Eq. (2.60)is derived as follows, once again by the virtue of Eq. (2.56)and the fact that
, appearing on the right‐hand side. The left‐hand side of Eq. (2.60)is derived as follows, once again by the virtue of Eq. (2.56)and the fact that  is the centre of mass:
is the centre of mass:
(2.61) 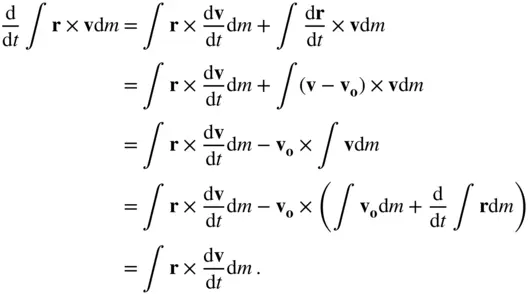
A substitution of Eq. (2.61)into Eq. (2.60)yields the following equation of rotational kinetics of the body:
(2.62) 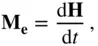
where
(2.63) 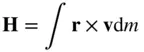
is the angular momentum of the body about its centre of mass, o . Thus a net external torque about the centre of mass of a body equals the time derivative of its angular momentum about the centre of mass.
If the body is rigid , then the distance between any two of its particles is a constant. Hence, the velocity of the elemental mass relative to 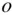 is given by
is given by
(2.64) 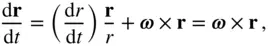
where 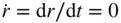 because
because 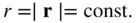 Here
Here  is the angular velocity of a local reference frame, oxyz , rigidly attached to the body at
is the angular velocity of a local reference frame, oxyz , rigidly attached to the body at 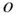 , with unit vectors
, with unit vectors 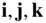 along
along 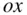 ,
, 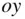 , and
, and 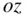 , respectively (Fig. 2.3), and is measured relative to the inertial frame, ( OXYZ ). Such a reference frame, oxyz , is termed a body‐fixed frame .
, respectively (Fig. 2.3), and is measured relative to the inertial frame, ( OXYZ ). Such a reference frame, oxyz , is termed a body‐fixed frame .
2.7 Gravity Field of a Body
The principles derived for the 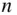 ‐body problem earlier in this chapter can be extended to the determination of the gravitational acceleration caused by a body whose mass,
‐body problem earlier in this chapter can be extended to the determination of the gravitational acceleration caused by a body whose mass, 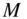 , is distributed over a large number of elemental masses,
, is distributed over a large number of elemental masses, 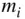 . In the following discussion, it is assumed that the other
. In the following discussion, it is assumed that the other 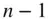 point masses are densely clustered together to form a body, away from the test mass,
point masses are densely clustered together to form a body, away from the test mass, 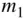 ; hence the test mass has the following equation of motion:
; hence the test mass has the following equation of motion:
Читать дальше

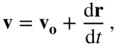
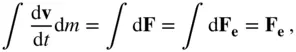
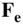 is the net external force acting on the body.
is the net external force acting on the body.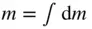 , of the body is a constant. This fact, along with Eq. (2.56), leads to the following:
, of the body is a constant. This fact, along with Eq. (2.56), leads to the following: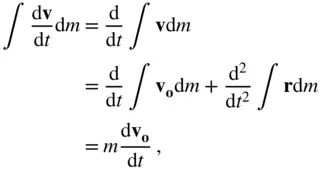
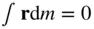 by the virtue of
by the virtue of 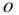 being the centre of mass of the body. Thus Eqs. ( 2.57) and ( 2.58) result in the following equation of the body's translation :
being the centre of mass of the body. Thus Eqs. ( 2.57) and ( 2.58) result in the following equation of the body's translation :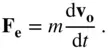

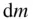 , with centre of mass o .
, with centre of mass o . , and integrating over the body as follows:
, and integrating over the body as follows: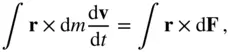
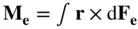 , appearing on the right‐hand side. The left‐hand side of Eq. (2.60)is derived as follows, once again by the virtue of Eq. (2.56)and the fact that
, appearing on the right‐hand side. The left‐hand side of Eq. (2.60)is derived as follows, once again by the virtue of Eq. (2.56)and the fact that 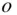 is the centre of mass:
is the centre of mass: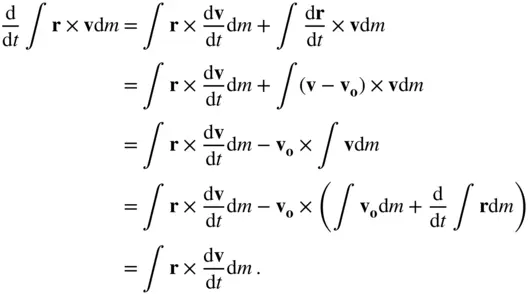
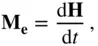
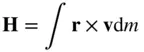
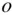 is given by
is given by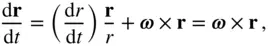
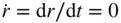 because
because 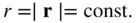 Here
Here  is the angular velocity of a local reference frame, oxyz , rigidly attached to the body at
is the angular velocity of a local reference frame, oxyz , rigidly attached to the body at 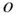 , with unit vectors
, with unit vectors 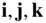 along
along 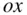 ,
, 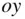 , and
, and 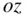 , respectively (Fig. 2.3), and is measured relative to the inertial frame, ( OXYZ ). Such a reference frame, oxyz , is termed a body‐fixed frame .
, respectively (Fig. 2.3), and is measured relative to the inertial frame, ( OXYZ ). Such a reference frame, oxyz , is termed a body‐fixed frame .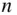 ‐body problem earlier in this chapter can be extended to the determination of the gravitational acceleration caused by a body whose mass,
‐body problem earlier in this chapter can be extended to the determination of the gravitational acceleration caused by a body whose mass, 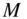 , is distributed over a large number of elemental masses,
, is distributed over a large number of elemental masses, 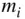 . In the following discussion, it is assumed that the other
. In the following discussion, it is assumed that the other 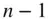 point masses are densely clustered together to form a body, away from the test mass,
point masses are densely clustered together to form a body, away from the test mass, 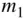 ; hence the test mass has the following equation of motion:
; hence the test mass has the following equation of motion:










