or
(2.54) 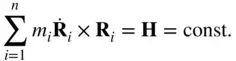
This implies that the 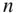 ‐particle motion takes place in a constant (or invariant ) plane containing the centre of mass. The constant vector
‐particle motion takes place in a constant (or invariant ) plane containing the centre of mass. The constant vector 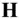 is normal to the invariant plane, and is termed the net angular momentum of the system about the origin
is normal to the invariant plane, and is termed the net angular momentum of the system about the origin 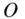 . This is the law of conservation of angular momentum in the absence of a net external torque about
. This is the law of conservation of angular momentum in the absence of a net external torque about 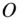 .
.
The conservation of linear and angular momentum, as well as the total energy of the 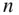 ‐particle system, is valid for any system ruled only by gravitational forces. The conservation principles are also valid for
‐particle system, is valid for any system ruled only by gravitational forces. The conservation principles are also valid for 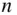 ‐bodies of arbitrary shapes, as no restrictions have been applied in deriving those principles for the
‐bodies of arbitrary shapes, as no restrictions have been applied in deriving those principles for the 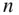 ‐particle system. A body is defined to be a collection of a large number of particles. Thus the particles can be grouped into several bodies, each translating and rotating with respect to a common reference frame. However, solving for the motion variables (linear and angular positions and velocities) of a system of
‐particle system. A body is defined to be a collection of a large number of particles. Thus the particles can be grouped into several bodies, each translating and rotating with respect to a common reference frame. However, solving for the motion variables (linear and angular positions and velocities) of a system of 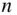 bodies (referred to as the
bodies (referred to as the 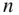 ‐ body problem ) requires a numerical determination of the individual gravity fields of the bodies, as well as an integration of the
‐ body problem ) requires a numerical determination of the individual gravity fields of the bodies, as well as an integration of the 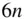 first‐order, ordinary differential equations governing their motion. The next section discusses how such differential equations are derived for a body. The solar system is an example of the
first‐order, ordinary differential equations governing their motion. The next section discusses how such differential equations are derived for a body. The solar system is an example of the 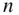 ‐body system. Numerical approximations and simplifying assumptions are invariably employed in the solution of the
‐body system. Numerical approximations and simplifying assumptions are invariably employed in the solution of the 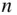 ‐body problem. For example, when the separations between the centres of mass of the respective bodies given by
‐body problem. For example, when the separations between the centres of mass of the respective bodies given by 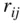 ,
, 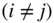 , are always large, the problem is approximated as that of
, are always large, the problem is approximated as that of 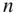 ‐bodies of spherical shape with radially symmetrical mass distributions.
‐bodies of spherical shape with radially symmetrical mass distributions.
The motion of a body is described by the motion of the particles constituting the body. A pure translation of a body is a motion in which all the particles constituting the body are moving in parallel straight lines with the same velocity. If the body is rigid, then the distance between any two of its particles is fixed; hence it is possible for the body to have a pure rotation , defined as the motion in which all the particles describe concentric circles about a fixed axis, and thus have velocities that are proportional to their respective distances from the axis of rotation. A rigid body in a combined translation and rotation has its constituent particles travelling in curved paths of different shapes relative to a stationary reference frame. A non‐rigid body can have structural deformation as it translates and rotates, wherein the relative distances of the particles varies with time. The general motion of a body therefore consists of a combination of translation, rotation, and structural deformation, whose complete description requires a determination of the spatial trajectories of the particles constituting the body.
Consider a body with the centre of mass, o , with a particle of elemental mass, d 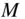 , located at
, located at 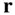 relative to o (see Fig. 2.3). Also consider an inertial reference frame, OXYZ , with origin at
relative to o (see Fig. 2.3). Also consider an inertial reference frame, OXYZ , with origin at 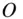 , and unit vectors,
, and unit vectors, 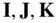 , along
, along 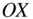 ,
, 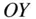 , and
, and 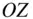 , respectively. The positions of o and the elemental mass relative to the origin,
, respectively. The positions of o and the elemental mass relative to the origin,  , are given by
, are given by 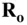 and
and 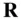 , respectively, whose time derivatives in the inertial frame are the respective velocities,
, respectively, whose time derivatives in the inertial frame are the respective velocities, 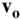 and
and 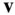 . If the net force experienced by the elemental mass is d
. If the net force experienced by the elemental mass is d 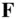 , then its equation of motion by Newton's second law is expressed as follows:
, then its equation of motion by Newton's second law is expressed as follows:
(2.55) 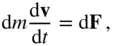
where the net force, d 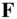 , is a sum of all internal (d
, is a sum of all internal (d 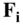 ) and external (d
) and external (d 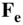 ) forces applied to the elemental mass,
) forces applied to the elemental mass, 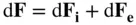 . The velocities,
. The velocities, 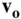 and
and 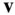 , are related by the following kinematic equation:
, are related by the following kinematic equation:
Читать дальше

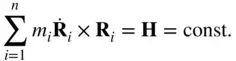
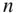 ‐particle motion takes place in a constant (or invariant ) plane containing the centre of mass. The constant vector
‐particle motion takes place in a constant (or invariant ) plane containing the centre of mass. The constant vector 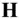 is normal to the invariant plane, and is termed the net angular momentum of the system about the origin
is normal to the invariant plane, and is termed the net angular momentum of the system about the origin 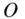 . This is the law of conservation of angular momentum in the absence of a net external torque about
. This is the law of conservation of angular momentum in the absence of a net external torque about 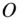 .
.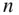 ‐particle system, is valid for any system ruled only by gravitational forces. The conservation principles are also valid for
‐particle system, is valid for any system ruled only by gravitational forces. The conservation principles are also valid for 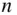 ‐bodies of arbitrary shapes, as no restrictions have been applied in deriving those principles for the
‐bodies of arbitrary shapes, as no restrictions have been applied in deriving those principles for the 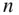 ‐particle system. A body is defined to be a collection of a large number of particles. Thus the particles can be grouped into several bodies, each translating and rotating with respect to a common reference frame. However, solving for the motion variables (linear and angular positions and velocities) of a system of
‐particle system. A body is defined to be a collection of a large number of particles. Thus the particles can be grouped into several bodies, each translating and rotating with respect to a common reference frame. However, solving for the motion variables (linear and angular positions and velocities) of a system of 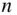 bodies (referred to as the
bodies (referred to as the 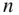 ‐ body problem ) requires a numerical determination of the individual gravity fields of the bodies, as well as an integration of the
‐ body problem ) requires a numerical determination of the individual gravity fields of the bodies, as well as an integration of the 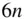 first‐order, ordinary differential equations governing their motion. The next section discusses how such differential equations are derived for a body. The solar system is an example of the
first‐order, ordinary differential equations governing their motion. The next section discusses how such differential equations are derived for a body. The solar system is an example of the 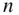 ‐body system. Numerical approximations and simplifying assumptions are invariably employed in the solution of the
‐body system. Numerical approximations and simplifying assumptions are invariably employed in the solution of the 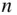 ‐body problem. For example, when the separations between the centres of mass of the respective bodies given by
‐body problem. For example, when the separations between the centres of mass of the respective bodies given by 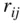 ,
, 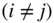 , are always large, the problem is approximated as that of
, are always large, the problem is approximated as that of 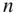 ‐bodies of spherical shape with radially symmetrical mass distributions.
‐bodies of spherical shape with radially symmetrical mass distributions.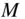 , located at
, located at 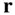 relative to o (see Fig. 2.3). Also consider an inertial reference frame, OXYZ , with origin at
relative to o (see Fig. 2.3). Also consider an inertial reference frame, OXYZ , with origin at 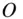 , and unit vectors,
, and unit vectors, 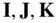 , along
, along 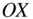 ,
, 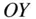 , and
, and 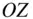 , respectively. The positions of o and the elemental mass relative to the origin,
, respectively. The positions of o and the elemental mass relative to the origin,  , are given by
, are given by 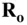 and
and 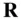 , respectively, whose time derivatives in the inertial frame are the respective velocities,
, respectively, whose time derivatives in the inertial frame are the respective velocities, 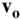 and
and 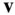 . If the net force experienced by the elemental mass is d
. If the net force experienced by the elemental mass is d 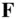 , then its equation of motion by Newton's second law is expressed as follows:
, then its equation of motion by Newton's second law is expressed as follows: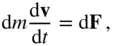
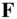 , is a sum of all internal (d
, is a sum of all internal (d 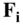 ) and external (d
) and external (d 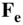 ) forces applied to the elemental mass,
) forces applied to the elemental mass, 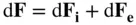 . The velocities,
. The velocities, 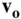 and
and 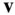 , are related by the following kinematic equation:
, are related by the following kinematic equation:










